ある条件を満たしたときのみ、回路に電流が流れないという現象が起きます。
ここではそんなブリッジ回路について解説します。
１．ブリッジ回路とは
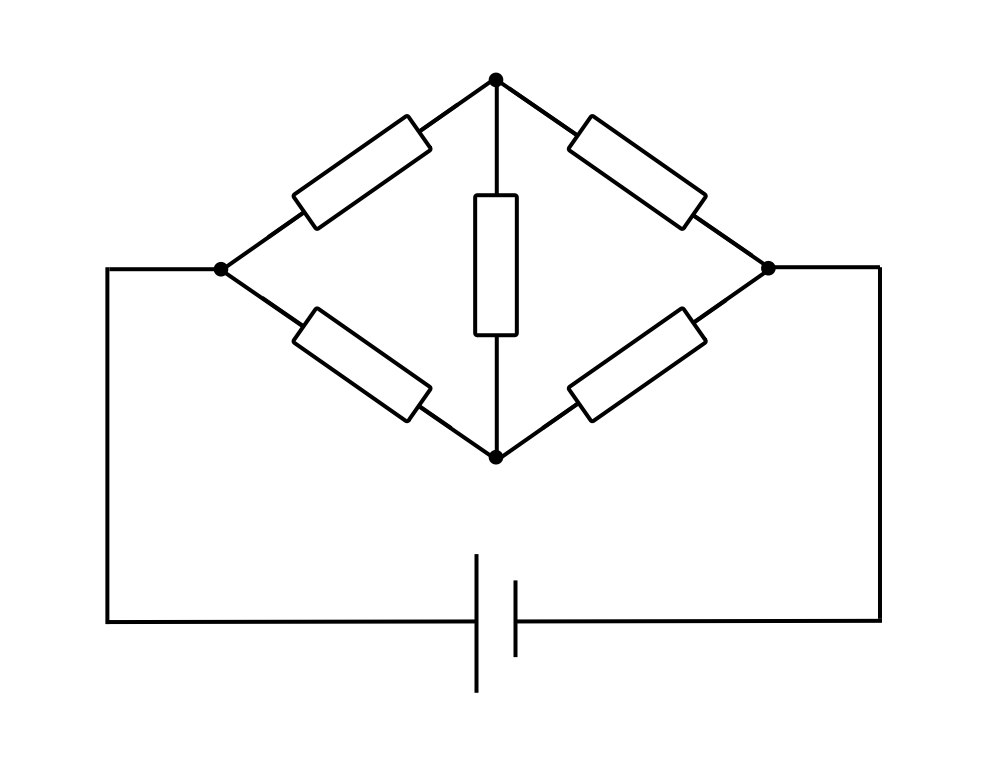
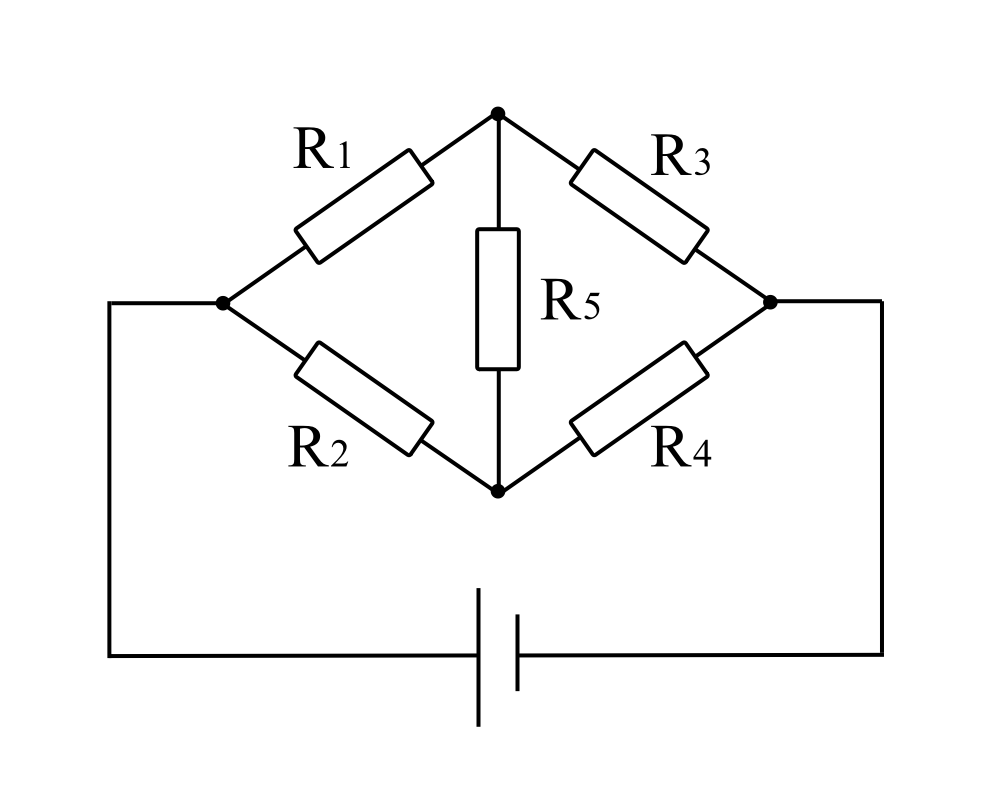
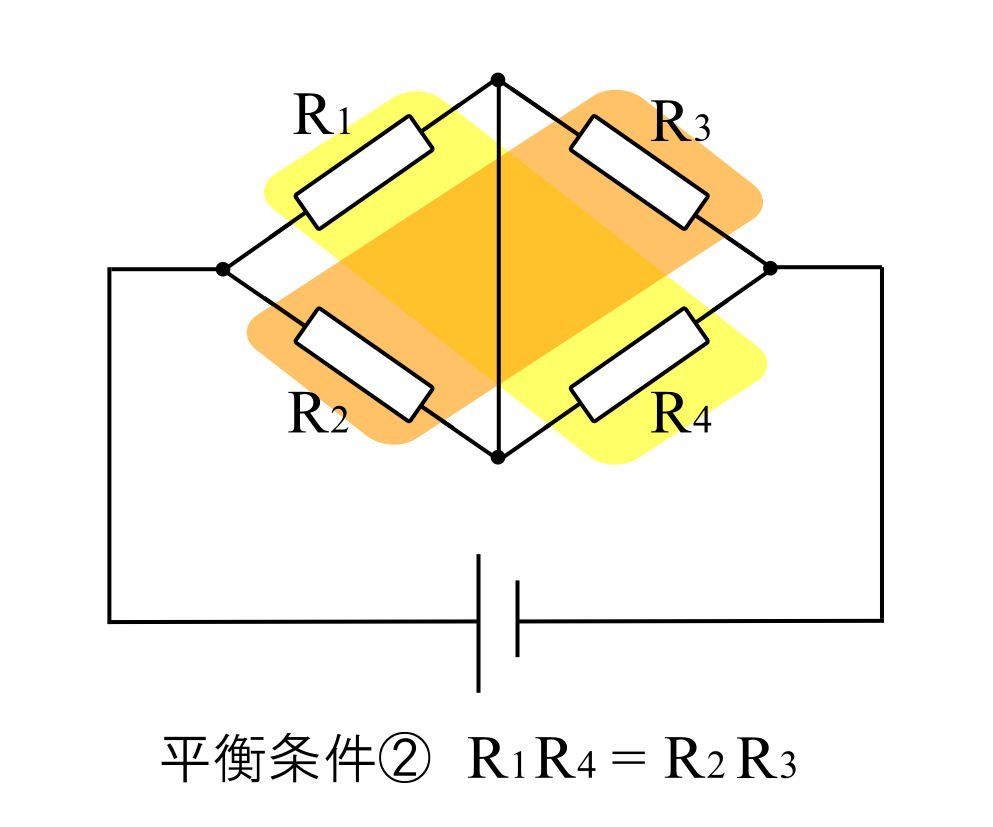
上記のような回路を、真ん中が橋渡しのようになっているので、ブリッジ回路と言います。
これはひし形で書かれることが多いのですが、変形すると並列回路に１本線を足しただけとも考えられます。
２．ブリッジ回路の平衡条件
（１）平衡条件とは
ブリッジ回路では、４つの抵抗\(R_1\)、\(R_2\)、\(R_3\)、\(R_4\)において、\(\displaystyle\frac{R_1}{R_2}=\displaystyle\frac{R_3}{R_4}\)が成り立つとき、抵抗\(R_5\)には電流が流れません。
これをブリッジ回路の平衡条件といいます。
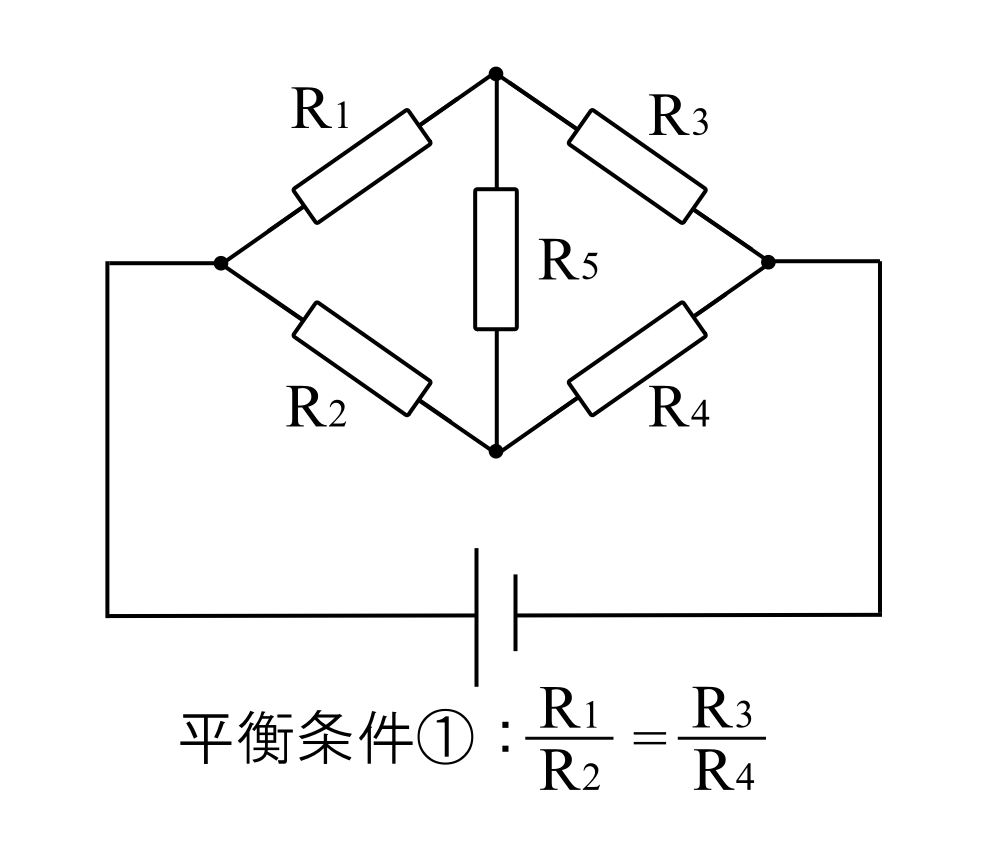
これは式を変更して、\(R_1R_4=R_2R_3\)としても同じです。
対角にある抵抗を組み合わせることを覚えると忘れにくいです。たすき掛けともいいます。
ブリッジ回路の平衡条件
次のような回路において
\(\displaystyle\frac{R_1}{R_2}=\displaystyle\frac{R_3}{R_4}\)
\(R_1R_4=R_2R_3\)
が成り立つとき\(R_5\)に電流は流れない
（２）平衡条件の証明
抵抗\(R_5\)に電流が流れないということは、点Bと点Cの電位は等しいということになります。
このことを仮定して電圧降下が等しいことを式にすると
\(R_1I_1=R_2I_2\) ・・・①
\(R_3I_3=R_4I_4\) ・・・②
また、\(R_5\)に電流が流れないということは、電流\(I_1\)、\(I_2\)、\(I_3\)、\(I_4\)については
\(I_1=I_3\) ・・・③
\(I_2=I_4\) ・・・④
となるため、式②に式③、④を代入すると
\(R_3I_1=R_4I_2\) ・・・⑤
となり、\(I_3\)と\(I_4\)が消えました。そして、式①÷式⑤とすることで
\(\displaystyle\frac{R_1I_1}{R_3I_1}=\displaystyle\frac{R_2I_2}{R_4I_2}\)
\(\displaystyle\frac{R_1}{R_3}=\displaystyle\frac{R_2}{R_4}\) ・・・⑥
となり、これを変形すると平衡条件である\(\displaystyle\frac{R_1}{R_2}=\displaystyle\frac{R_3}{R_4}\)と、\(R_1R_4=R_2R_3\)が導けます。
よって、この平衡条件の時に点B点とC間の電位差がなくなり、電流が流れないことが証明できます。
３．例題（第一種電気工事士試験）
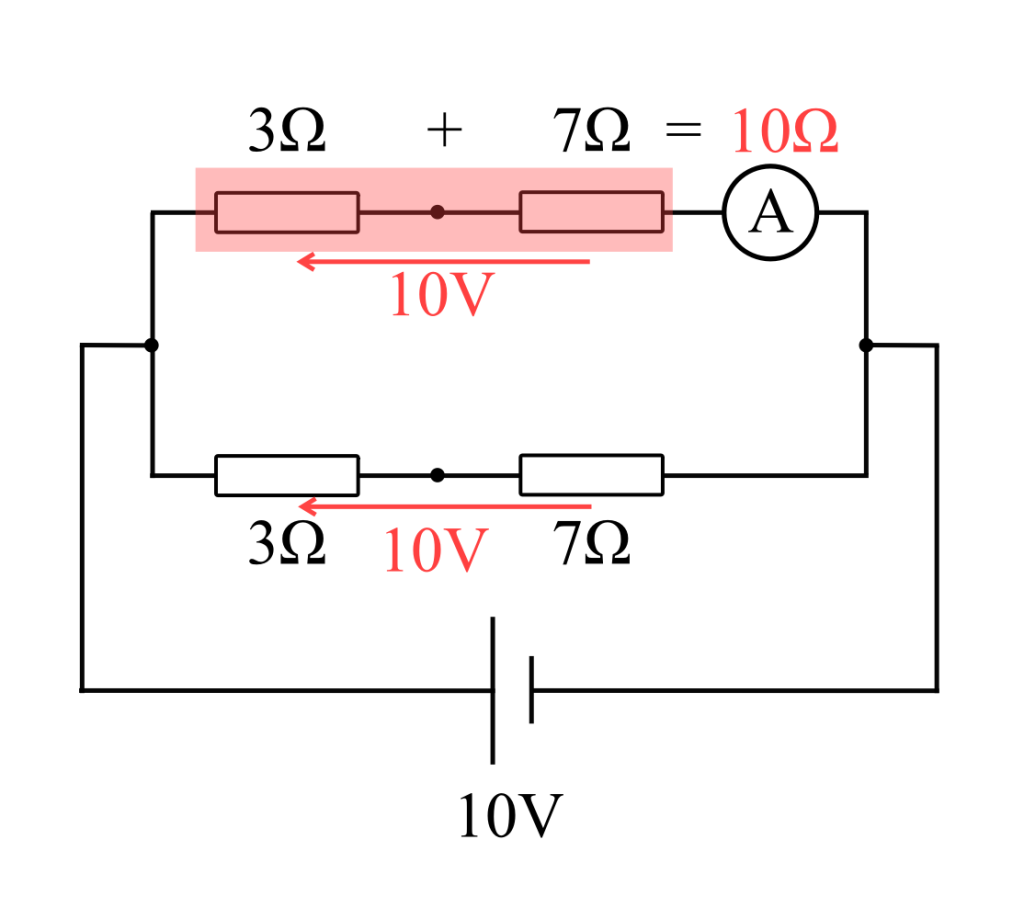
図のような直流回路において、電流計に流れる電流[A]は。
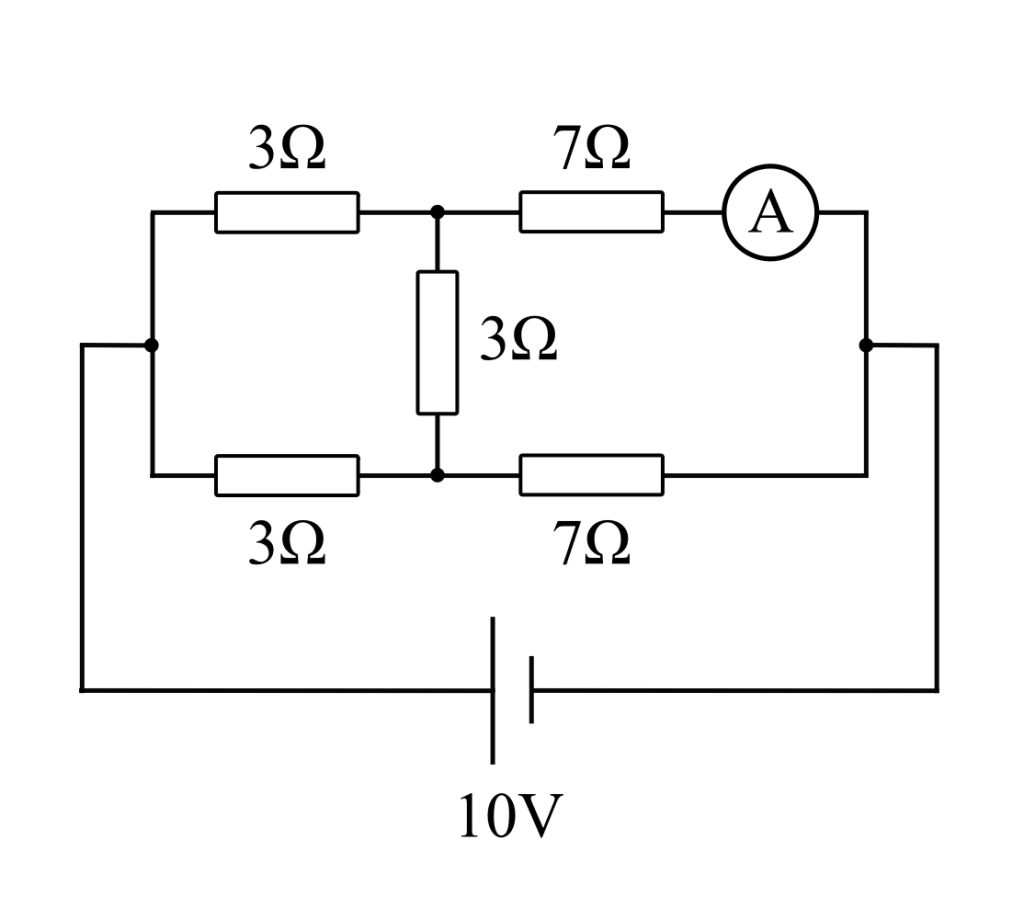
答え：ハ
【解説】
抵抗の並列接続の部分に注目するとブリッジ回路になっていることがわかります。
そのため真ん中の3Ωの抵抗に電流は流れず、単純な並列回路とみなすことができます。
電源電圧が10V、並列回路なので電流計のある側の抵抗に対しても10Vの電圧がかかる為、オームの法則より、
\(I=\displaystyle\frac{V}{R}=\displaystyle\frac{10}{10}=1\)
よって答えは1[A]となります。
