１．分圧の法則（抵抗が２つ）
（１）電圧のかかる抵抗の大きさに比例して分かれる
分圧とは、以下のような直流直列回路で、それぞれの抵抗に電源電圧が分かれることです。
分かれる電圧の比率は、抵抗の大きさの比に等しくなります。
分圧の法則（抵抗が２つの場合）
分圧の比は、かかる抵抗の比に等しくなる
→抵抗の比が\(R_1:R_2\)の場合、電圧の比は\(V_1:V_2\)となる
（２）なぜ抵抗の比に等しくなるのか？
以下のような直流直列回路を考えます。
ポイントは電流\(I\)がどこでも同じ大きさということ
電流\(I\)は回路のどこでも一定なので、\(R_1\)、\(R_2\)に流れる電流はどちらも\(2\)Aです。
抵抗\(R_1\)と\(R_2\)、それぞれにかかる電圧\(V_1\)、\(V_2\)を、オームの法則を使って解きます。
\(V=I×R\)より
\(V_1=I×R_1=2×4=8\) [V]、\(V_2=I×R_2=2×8=16\) [V]
抵抗と電圧の比をくらべると
\(R1:R2=4:8=1:2\)
\(V_1:V_2=8:16=1:2\)
このように、直列回路における抵抗に分圧した電圧の比は、抵抗の比と等しくなります。
２．分圧の法則（抵抗が３つ以上）
抵抗が３つ以上ある場合の考え方です。
直列回路の合成抵抗は単純に足していけばいいので、抵抗がn個の回路の合成抵抗は
\(R_0=R_1+R_2+R_3・・・+R_n\)
回路電流は以下の式で表すことができます。
\(I=\displaystyle\frac{E}{R_0}\)
抵抗\(R_1\)に係る電圧\(V_1\)はオームの法則より
\(V_1=IR_1\)
これに\(I=\displaystyle\frac{E}{R_0}\)を代入すると
\(V_1=E×\displaystyle\frac{R_1}{R_0}\)
となります。
他の抵抗も同様に表すことができます。
\(V_1=E×\displaystyle\frac{R_1}{R_0}\)
\(V_2=E×\displaystyle\frac{R_2}{R_0}\)
\(V_3=E×\displaystyle\frac{R_3}{R_0}\)
：
\(V_n=E×\displaystyle\frac{R_n}{R_0}\)
このように、抵抗\(R_n\)に分圧した電圧\(V_n\)を求めたい場合、電源電圧\(E\)に\(\displaystyle\frac{対象の抵抗R_n}{合成抵抗R_0}\)を掛けることで求められます。
分圧の法則（抵抗が３つ以上の場合）
\(V_n=E×\displaystyle\frac{R_n}{R_0}\)
\(V_n\)：抵抗\(R_n\)に分圧した電圧[V] \(R_n\)：求めたい電圧のかかる抵抗[Ω]
\(R_0\)：回路の合成抵抗[Ω] \(E\)：電源電圧[V]
３．例題
図のような直流回路で、a-b間の電圧[V]は。
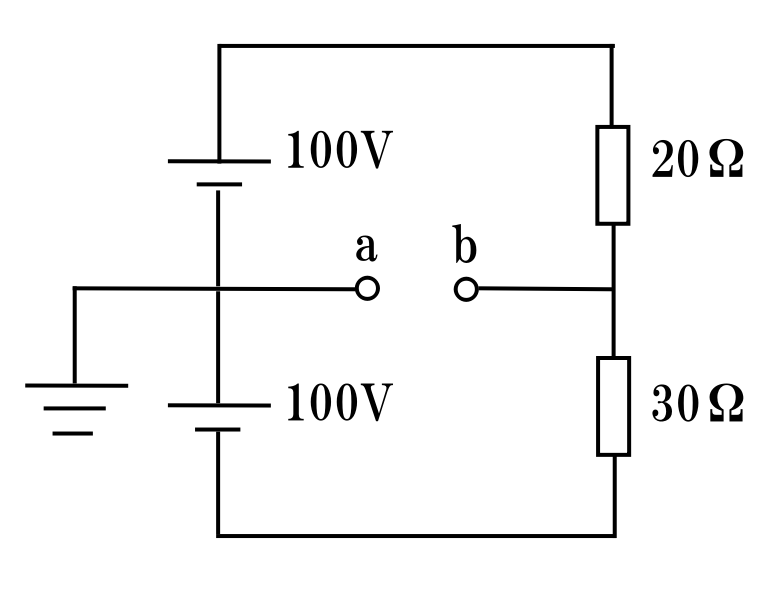
イ．10 ロ．20 ハ．30 ニ．40
答え：ロ
（解説）
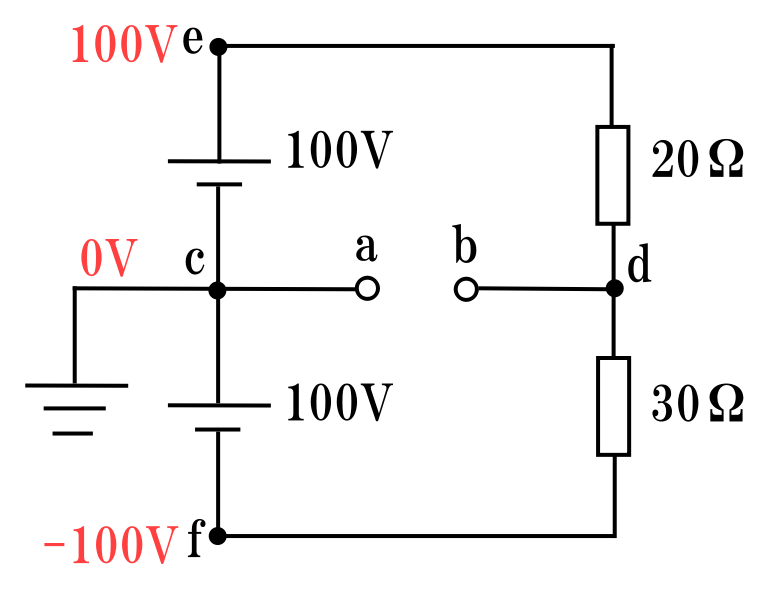
図のように点c～fをおいて考えます。
まず、点cの電位は接地されているので\(0V\)です。
また、点eの電位は\(100V\)、点fの電位は\(-100V\)となります。
電源電圧は\(100V\)が２つ直列に繋がっているので、合わせて\(200V\)になります。
直列回路なので、合成抵抗は
\(20+30=50[Ω]\)
となります。
分圧の法則を使い、\(20Ω\)の抵抗にかかる電圧は
\(200×\displaystyle\frac{20}{50}=80[V]\)
とわかります。
これは\(80V\)の電圧降下なので、点dの電位は
\(100-80=20[V]\)
点bと点dは同じ電位なので\(20V\)、点aと点cの電位は\(0V\)です。
そのため、点a-b間の電圧
\(20-0=20[V]\)
答えはロの\(20[V]\)となります。