

今回のテーマは交流回路の計算。
電気工事士などの試験でも必須の知識だよ。

交流回路ではコイルとコンデンサの計算が複雑だよね?
それとインピーダンスって何だっけ?

じゃあ、今回は電流の流れを妨げるインピーダンス(抵抗・コイル・コンデンサ)の計算方法について解説するよ。
コイルやコンデンサを含んだ交流回路の計算方法を解説します。
オームの法則や合成抵抗の求め方については、他の記事で解説しているのでよく理解していない人はご覧下さい。
1.インピーダンスとは?
抵抗のように電流の流れを妨げる性質を持つものをインピーダンスと呼びます。記号は\(Z\)、単位はΩ(オーム)を使います。
インピーダンスには抵抗、コイル(誘導性リアクタンス)、コンデンサ(容量性リアクタンス)の3つがあります。
これらの異なる成分を合成して表すことから、合成インピーダンスとも呼びます。
インピーダンスは抵抗と同じようにオームの法則が成り立ちます。
2.抵抗の計算方法
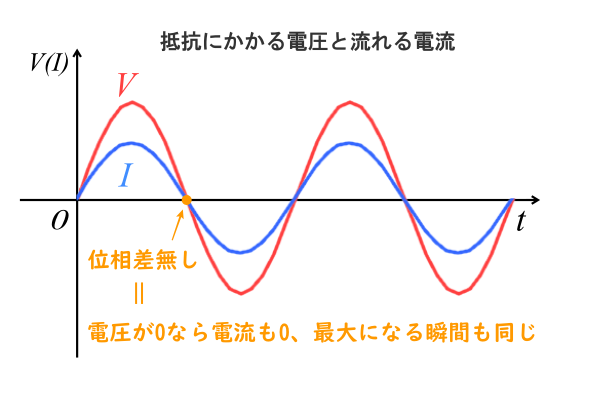
抵抗は電圧と電流の位相が一致しているので、直流と同じように計算できます。
電圧\(V\)と電流\(I\)の位相(時間的変化)をグラフにすると以下のようになります。
2.コイルの特性と計算方法
(1)コイルの特性
ⅰ.直流の場合
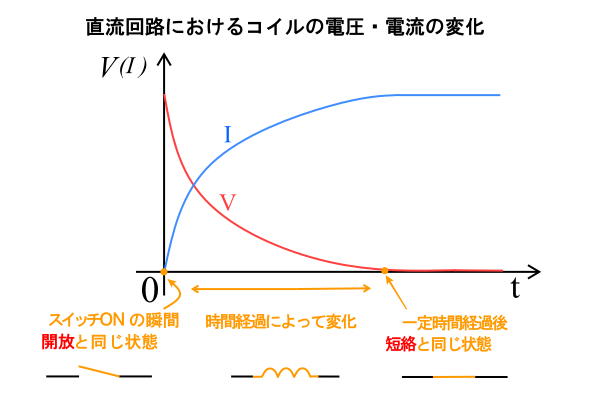
コイルは直流の場合、電流の流し始めは開放と同じ状態になります。(電流が流れない・電圧は最大・抵抗は無限大)
電流は徐々に流れるようになり、最終的には短絡と同じ状態になります。(電流は最大・電圧はゼロ・抵抗はゼロ)
ⅱ.交流の場合
交流は直流と異なり、絶えず向きが変わります。
コイルには変化を嫌う性質がある為、電圧をかけてすぐには電流は流れず、徐々に流れるようになります。
電圧がプラスからゼロに変化する際も、蓄えたエネルギーで電流はプラスの向きに流れ続けます。
電圧がマイナスになってもしばらく電流はそのままプラスの向きに流れます。
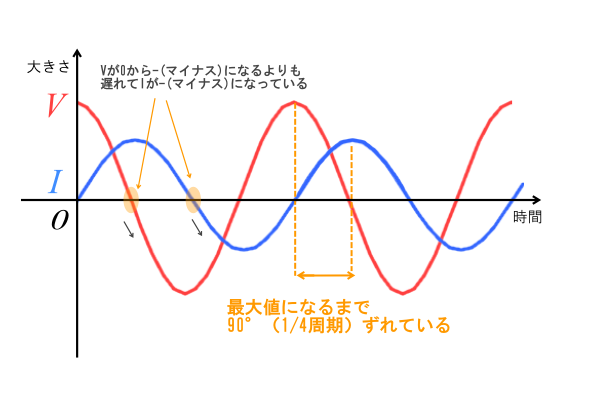
このためコイルに流れる電流は電圧よりも位相の(時間的に)遅れた電流が流れます。
逆に言うと、コイルにかかる電圧は電流に対して位相が進みます。
(2)コイルを含む直列回路の合成インピーダンス(RL直列回路)
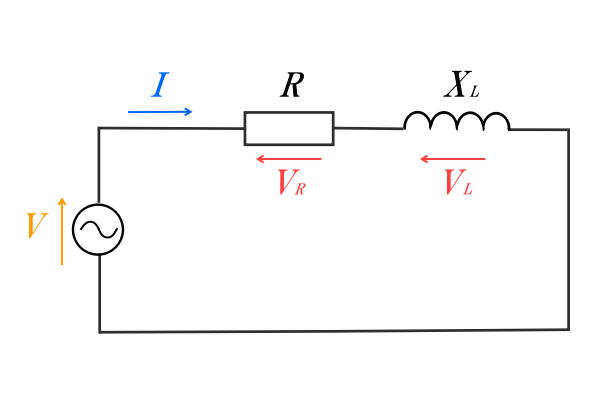
抵抗\(R\)とコイル\(X_L\)からなる直列回路を考えます。
(\(R\)、\(X_L\)にかかる電圧は電圧降下を意味しているので電源電圧とは逆向きの矢印になります。)
抵抗をR、コイルLとして、RL直列回路ともいいます。
抵抗とコイルは位相が異なるので、単純に足し合わすことはできません。
大きさだけでなく、向きも計算するため、ベクトル図を書いて考えます。
直列の場合、抵抗に流れる電流とコイルに流れる電流が同じなので、電流の位相を基準ベクトルとして、各要素にかかる電圧についてベクトル図を書きます。

① 電流\(I\)の位相を基準ベクトルとして原点Oからx軸方向に右向きのベクトルを書きます。
② 抵抗にかかる電圧\(V_R\)は電流と位相が同じため、電流\(I\)と同じくx軸方向に右向きのベクトルを書きます。
③ コイルにかかる電圧\(V_L\)は電流に対して90°進む(逆に電流から見ると電圧に対して遅れる)ため、y軸方向に上向きのベクトルを書きます。
④ \(V_R\)、\(V_L\)を含む長方形を書き、原点Oから対角線になるベクトルを書きます。これが回路全体にかかる電圧\(V\)になります。
回路全体にかかる電圧\(V\)の大きさは\(V_R\)、\(V_L\)それぞれの二乗を足し合わせて平方根をとることで求められます。
\(V=\sqrt{V_R^2+V_L ^2}\)
\(=\sqrt{(IR)^2+(IX_L)^2}\)
\(=I\sqrt{R^2+X_L^2}\)
\(V=IZ\)なので、合成インピーダンス\(Z\)は\(\sqrt{R^2+X_L^2}\)と求められます。
(3)コイルを含む並列回路の合成インピーダンス(RL並列回路)
続いて、抵抗とコイルからなる並列回路の場合を見ていきます。
こちらは抵抗をR、コイルLとして、RL並列回路ともいいます。
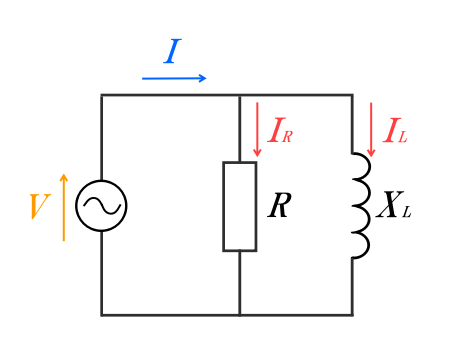
並列回路の場合、それぞれの要素にかかる電圧は同じで、電流はそれぞれに分かれるようになります。
ここでそれぞれに流れる電流は
\(I_R=\displaystyle\frac{V}{R}\)
\(I_L=\displaystyle\frac{V}{X_L}\)
となりますが、これらは位相が異なるので、今度は電圧を基準ベクトルとして、各要素に流れる電流についてのベクトル図を書きます。
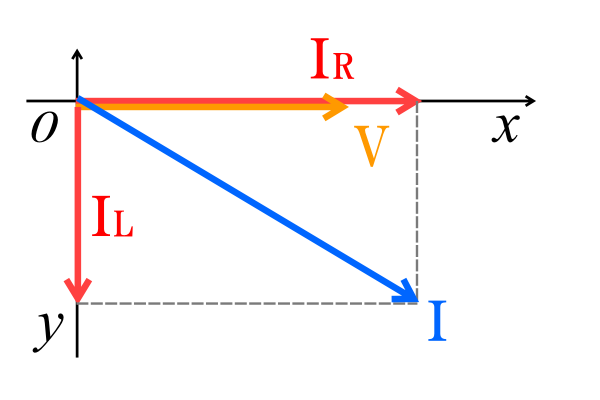
① 電圧\(V\)の位相を基準ベクトルとして原点Oからx軸方向に右向きのベクトルを書きます。
② 抵抗に流れる電流\(I_R\)は電圧と位相が同じため、電圧\(V\)と同じくx軸方向に右向きのベクトルを書きます。
③ コイルに流れる電流\(I_L\)は電圧に対して90°遅れる(逆に電圧から見ると電流に対して進む)ため、y軸方向に下向きのベクトルを書きます。
④ \(I_R\)、\(I_L\)を含む長方形を書き、原点Oから対角線になるベクトルを書きます。これが回路全体に流れる電流\(I\)になります。
回路全体に流れる電流\(I\)は以下のように計算できます。
\(I=\sqrt{I_R^2+I_L^2}\)
\(=\sqrt{\displaystyle\left(\frac{V}{R}\right)^2+\displaystyle\left(\frac{V}{X_L}\right)^2}\)
\(=V\sqrt{\displaystyle\left(\frac{1}{R}\right)^2+\displaystyle\left(\frac{1}{X_L}\right)^2}\)
電流 \(I\)は \(I=\displaystyle\frac{V}{Z}\)なので、電圧 \(V\)に対して合成インピーダンスの逆数 \(\displaystyle\frac{1}{Z}\)を掛けたものとなります。
式を \(\displaystyle\frac{1}{Z}=\)の形に変形すると
\(\displaystyle\frac{1}{Z}=\sqrt{\displaystyle\left(\frac{1}{R}\right)^2+\displaystyle\left(\frac{1}{X_L}\right)^2}\)
よって、合成インピーダンス\(Z\)は以下のように求めることができます。
\(Z=\displaystyle\frac{1}{(\frac{1}{Z})}=\displaystyle\frac{1}{\sqrt{(\frac{1}{R})^2+(\frac{1}{X_L})^2}}\)
合成抵抗の求め方同様、並列の場合は逆数の和の逆数が合成インピーダンスとなることがわかります。
3.コンデンサの特性と計算方法
(1)コンデンサの特性
ⅰ.直流の場合
コンデンサは直流の場合、電流の流し始めは導体と同じ状態になります。(電流が最大・無電圧・抵抗がゼロ)
電流はコンデンサ内部に充電されて、最終的にはこれ以上充電できないという状態になり、開放と同じ状態になります。(電流が流れない・電圧最大・抵抗は無限大)
.png)
ⅱ.交流の場合
コンデンサは、電圧がかかってすぐは電流を流しますが、次第に充電された電荷で満たさるため、電流は流れなくなります。
交流の場合は、この動きがプラスとマイナスで方向を変えて続いていきます。
電圧がプラスからゼロへ小さくなる時、コンデンサは充電した向きとは逆方向に(ゼロからマイナスへ)放電します。
電圧がゼロからマイナスの向きに増大するときは、コンデンサは充電になる為、流れる電流は小さくなります。(やがてゼロになります)
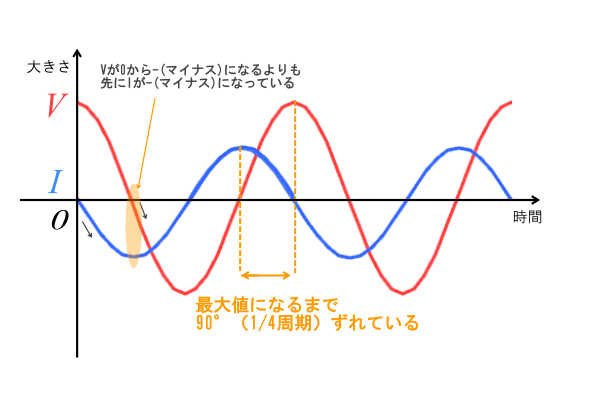
このためコンデンサに流れる電流は電圧よりも位相の(時間的に)進んだ電流が流れます。
逆に言うと、コイルにかかる電圧は電流に対して位相が遅れます。
(2)コンデンサを含む回路の合成インピーダンス(RC直列回路)
抵抗とコンデンサからなる直列回路を考えます。
抵抗をR、コンデンサをCとして、RC直列回路ともいいます。
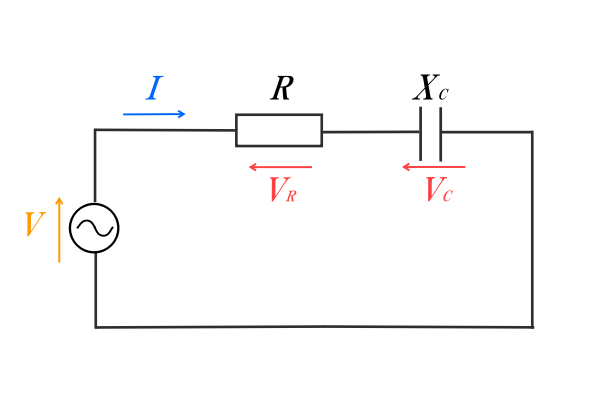
抵抗とコンデンサは位相が異なるので、単純に足し合わすことはできません。
この場合も大きさだけでなく、向きも計算するため、ベクトル図を書いて考えます。
直列の場合、抵抗に流れる電流とコンデンサに流れる電流が同じなので、電流の位相を基準ベクトルとして各要素にかかる電圧についてベクトル図を書きます。

① 電流\(I\)の位相を基準ベクトルとして原点Oからx軸方向に右向きのベクトルを書きます。
② 抵抗にかかる電圧\(V_R\)は電流と位相が同じため、電流\(I\)と同じくx軸方向に右向きのベクトルを書きます。
③ コンデンサにかかる電圧\(V_C\)は電流に対して90°遅れる(逆に電流から見ると電圧に対して進む)ため、y軸方向に下向きのベクトルを書きます。
④ \(V_R\)、\(V_C\)を含む長方形を書き、原点Oから対角線になるベクトルを書きます。これが回路全体にかかる電圧\(V\)になります。
回路全体にかかる電圧\(V\)の大きさは\(V_R\)、\(V_C\)それぞれの二乗を足し合わせて平方根をとることで求められます。
\(V=\sqrt{V_R^2+V_C ^2}\)
\(=\sqrt{(IR)^2+(IX_C)^2}\)
\(=I\sqrt{R^2+X_C^2}\)
\(V=IZ\)なので、合成インピーダンスZは\(\sqrt{R^2+X_C^2}\)と求められます。
(3)コンデンサを含む回路の合成インピーダンス(RC並列回路)
続いて、抵抗とコンデンサからなる並列回路を考えます。
抵抗をR、コンデンサをCとして、RC並列回路ともいいます。
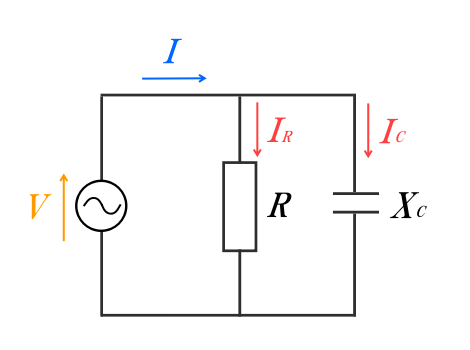
RL並列回路と同様、それぞれの要素にかかる電圧は同じで、電流はそれぞれに分かれるようになります。
ここでそれぞれに流れる電流は
\(I_R=\displaystyle\frac{V}{R}\)
\(I_C=\displaystyle\frac{V}{X_C}\)
となりますが、これらは位相が異なるので、今度は電圧を基準ベクトルとして、各要素に流れる電流についてのベクトル図を書きます。
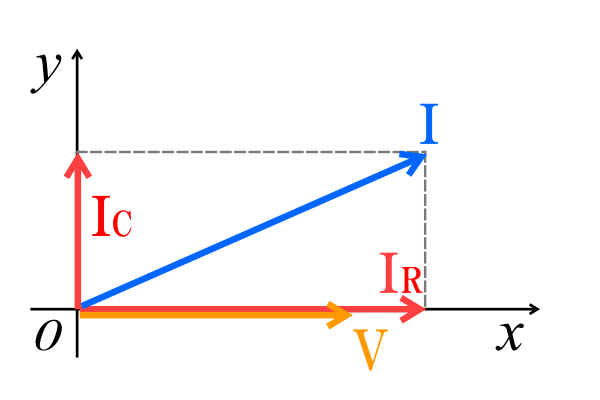
① 電圧\(V\)の位相を基準ベクトルとして原点Oからx軸方向に右向きのベクトルを書きます。
② 抵抗に流れる電流\(I_R\)は電圧と位相が同じため、電圧\(V\)と同じくx軸方向に右向きのベクトルを書きます。
③ コンデンサに流れる電流\(I_C\)は電圧に対して90°進む(逆に電圧から見ると電流に対して遅れる)ため、y軸方向に上向きのベクトルを書きます。
④ \(I_R\)、\(I_C\)を含む長方形を書き、原点Oから対角線になるベクトルを書きます。これが回路全体に流れる電流\(I\)になります。
回路全体に流れる電流\(I\)は以下のように計算できます。
\(I=\sqrt{I_R^2+I_C^2}\)
\(=\sqrt{\displaystyle\left(\frac{V}{R}\right)^2+\displaystyle\left(\frac{V}{X_C}\right)^2}\)
\(=V\sqrt{\displaystyle\left(\frac{1}{R}\right)^2+\displaystyle\left(\frac{1}{X_C}\right)^2}\)
電流 \(I\)は \(I=\displaystyle\frac{V}{Z}\)なので、電圧 \(V\)に対して合成インピーダンスの逆数 \(\displaystyle\frac{1}{Z}\)を掛けたものとなります。
式を \(\displaystyle\frac{1}{Z}=\)の形に変形すると
\(\displaystyle\frac{1}{Z}=\sqrt{\displaystyle\left(\frac{1}{R}\right)^2+\displaystyle\left(\frac{1}{X_C}\right)^2}\)
よって、合成インピーダンス\(Z\)は以下のように求めることができます。
\(Z=\displaystyle\frac{1}{\sqrt{(\frac{1}{R})^2+(\frac{1}{X_C})^2}}\)
合成抵抗の求め方同様、並列の場合は逆数の和の逆数が合成インピーダンスとなることがわかります。
4.コイルとコンデンサを含む合成インピーダンスの求め方
(1)RLC直列回路の合成インピーダンス
抵抗・コイル・コンデンサを含む直列回路は以下のように表します。
抵抗をR、コイルをL、コンデンサをCとして、RLC直列回路ともいいます。
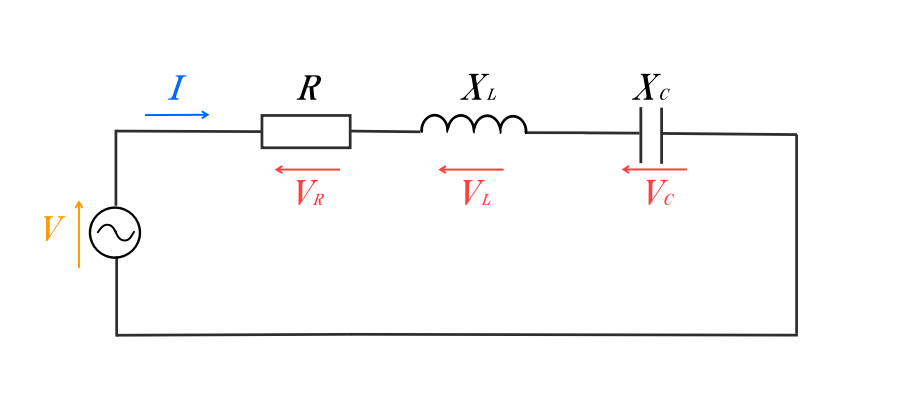
RL直列回路、RC直列回路のときと同様、電流\(I\)が共通している為、電流を基準ベクトルとしてベクトル図を書きます。

① 電流\(I\)の位相を基準ベクトルとして原点Oからx軸方向に右向きのベクトルを書きます。
② 抵抗にかかる電圧\(V_R\)は電流と位相が同じため、電流\(I\)と同じくx軸方向に右向きのベクトルを書きます。
③ コイルにかかる電圧\(V_L\)は電流に対して90°進む(逆に電流から見ると電圧に対して遅れる)ため、y軸方向に上向きのベクトルを書きます。
④ コンデンサにかかる電圧\(V_C\)は電流に対して90°遅れる(逆に電流から見ると電圧に対して進む)ため、y軸方向に下向きのベクトルを書きます。
⑤ コイルにかかる電圧\(V_L\)とコンデンサにかかる電圧\(V_C\)は互いに相殺するので、大きい方の向きにベクトルを書きます。(この場合は\(V_L-V_C\)となり、y軸方向に上向き)
⑥ \(V_R\)、\(V_L-V_C\)を含む長方形を書き、原点Oから対角線になるベクトルを書きます。これが回路全体にかかる電圧\(V\)になります。
上記はコイルの方が大きい場合ですが、コンデンサが大きい場合は\(V_L\)と\(V_C\)の合成ベクトルは逆向きになります。
回路全体にかかる電圧の大きさは以下のように求められます。
\(V=\sqrt{V_R^2+(V_L-V_C)^2}\)
\(=\sqrt{(IR)^2+(IX_L-IX_C)^2}\)
\(=I\sqrt{R^2+(X_L-X_C)^2}\)
\(V=IZ\)(オームの法則)より、回路全体にかかる電圧\(V\)を電流\(I\)で割ることで合成インピーダンス\(Z\)が求められます。
\(Z=\sqrt{R^2+(X_L-X_C)^2}\)
(2)RLC並列回路の合成インピーダンス
抵抗・コイル・コンデンサを含む並列回路は以下のように表します。
抵抗をR、コイルをL、コンデンサをCとして、RLC並列回路ともいいます。
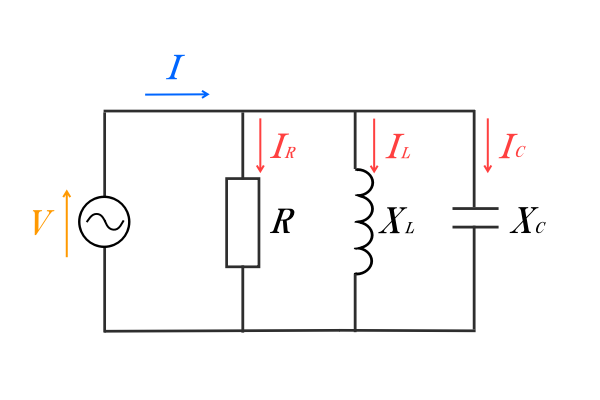
RL並列回路、RC並列回路のときと同様、電圧が共通している為、電圧を基準ベクトルとしてベクトル図を書きます。
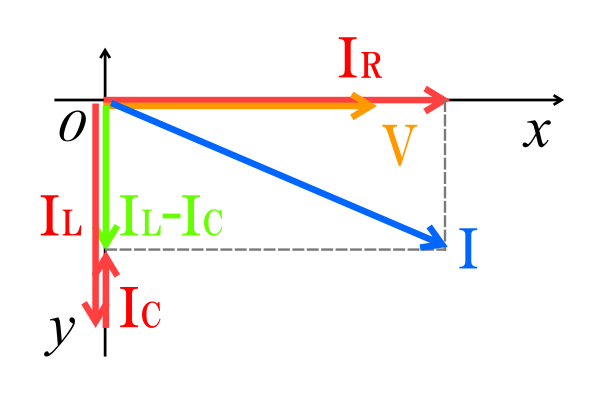
① 電圧\(V\)の位相を基準ベクトルとして原点Oからx軸方向に右向きのベクトルを書きます。
② 抵抗にかかる電流\(I_R\)は電圧と位相が同じため、電圧\(V\)と同じくx軸方向に右向きのベクトルを書きます。
③ コイルに流れる電流\(I_L\)は電圧に対して90°遅れる(逆に電流から見ると電圧に対して進む)ため、y軸方向に下向きのベクトルを書きます。
④ コンデンサに流れる電流\(I_C\)は電圧に対して90°進む(逆に電流から見ると電圧に対して遅れる)ため、y軸方向に上向きのベクトルを書きます。
⑤ コイルに流れる電流\(I_L\)とコンデンサに流れる電流\(I_C\)は互いに相殺するので、大きい方の向きにベクトルを書きます。(この場合は\(I_L-I_C\)となり、y軸方向に下向き)
⑥ \(I_R\)、\(I_L-I_C\)を含む長方形を書き、原点Oから対角線になるベクトルを書きます。これが回路全体に流れる電流\(I\)になります。
上記はコイルの方が大きい場合ですが、コンデンサが大きい場合は\(I_L\)と\(I_C\)の合成ベクトルは逆向きになります。
回路全体に流れる電流の大きさは以下のように求められます。
\(I=\sqrt{I_R^2+(I_L-I_C)^2}\)
\(=\sqrt{\displaystyle\left(\frac{V}{R}\right)^2+\displaystyle\left(\frac{V}{X_L}-\frac{V}{X_C}\right)^2}\)
\(=V\sqrt{\displaystyle\left(\frac{1}{R}\right)^2+\displaystyle\left(\frac{1}{X_L}-\frac{1}{X_C}\right)^2}\)
\(I=\displaystyle\frac{V}{Z}\)(オームの法則)より、上記の式を電圧\(V\)で割ると、合成インピーダンスの逆数\(\displaystyle\frac{1}{Z}\)となります。
\(\displaystyle\frac{1}{Z}=\sqrt{\displaystyle\left(\frac{1}{R}\right)^2+\displaystyle\left(\frac{1}{X_L}-\frac{1}{X_C}\right)^2}\)
そしてこの逆数が合成インピーダンス\(Z\)となります。
\(Z=\displaystyle\frac{1}{\sqrt{\displaystyle\left(\frac{1}{R}\right)^2+\displaystyle\left(\frac{1}{X_L}-\frac{1}{X_C}\right)^2}}\)
こちらも合成抵抗と同じく、並列回路は逆数の和の逆数を取ることで合成インピーダンスを求めますが、二乗して平方根を取らなければならない点は注意が必要です。
5.まとめ
交流回路は位相を考慮しなければならず、計算が複雑になります。
慣れないうちはベクトル図を書いてから計算するといいと思います。
今回の計算式を以下にまとめます。(順番は変えています)
<<第二種電気工事士試験についての情報はこちら>>
<<第一種電気工事士試験についての情報はこちら>>





