
抵抗が複数ある場合、これを1つにまとめてから他の計算をします。
まとめた抵抗を合成抵抗といいますが、これは直列の場合と並列の場合で計算方法が異なります。
オームの法則についてはこちらの記事で説明しております。
1.合成抵抗の求め方(直列)
直列の場合は以下のように求めます。
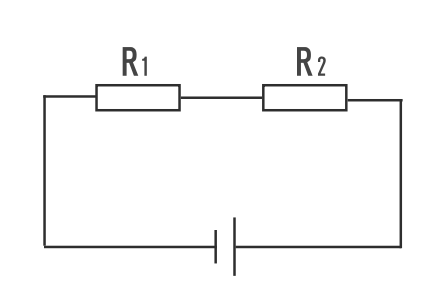
R=R1+R2
R:合成抵抗 R1:抵抗1 R2:抵抗2
直列の場合はそのまま足し算でOKです。
1.合成抵抗の求め方(並列)
並列の場合は以下のように求めます。
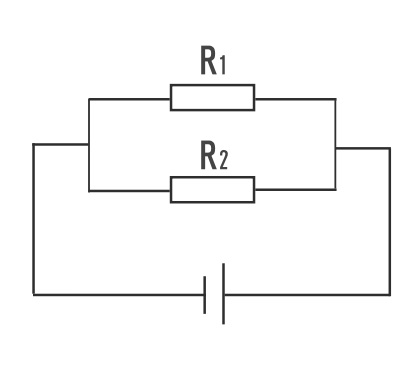
合成したい抵抗の逆数を分母に置いて足し合わせ、それの逆数を取るという計算です。
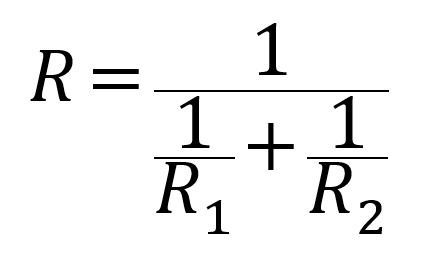
R:合成抵抗 R1:抵抗1 R2:抵抗2
また、2つの抵抗の合成抵抗であれば、通称「和分の積」でも求められます。
分母が2つの和で、分子が2つの積なのでこう呼ばれています。こちらの方が易しいです。
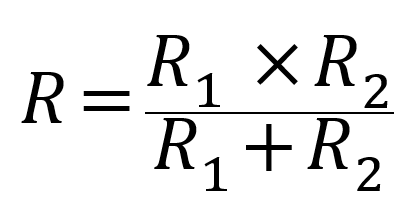
R:合成抵抗 R1:抵抗1 R2:抵抗2
3.例題
例題
以下の回路に流れる電流Iを求めよ
-1.png)
以下のように直列、並列が組み合わさった回路の場合は順番に計算します。
①並列部分の合成抵抗を求める
和分の積を使い、(6×2)÷(6+2)=1.5 となり、並列の合成抵抗は1.5[Ω]だとわかります。
②直列部分の合成抵抗を求める
直列部分はそのまま足せばいいので、3+1.5=4.5となり、回路全体の合成抵抗は4.5[Ω]だと分かります。
③オームの法則で電圧÷合成抵抗を求める
求めたい電流値はオームの法則より、9[V]÷4.5[Ω]=2[A]となります。
よって答えは 2[A(アンペア)]となります
この計算ができれば、簡易的な人体の感電の計算も可能です。(人体の抵抗値と接地抵抗値の合成抵抗値)



