
今回は使用電力量の計算で重要な分野である
需要率・不等率・負荷率について解説します。
混同しないように注意しましょう。
1.需要率
(1)最大需要電力とは
「需要電力」とは、使った電力や使う見込みの電力のことです。
一般的には1時間あたりで平均何ワット使ったかのことを指すことが多いです。
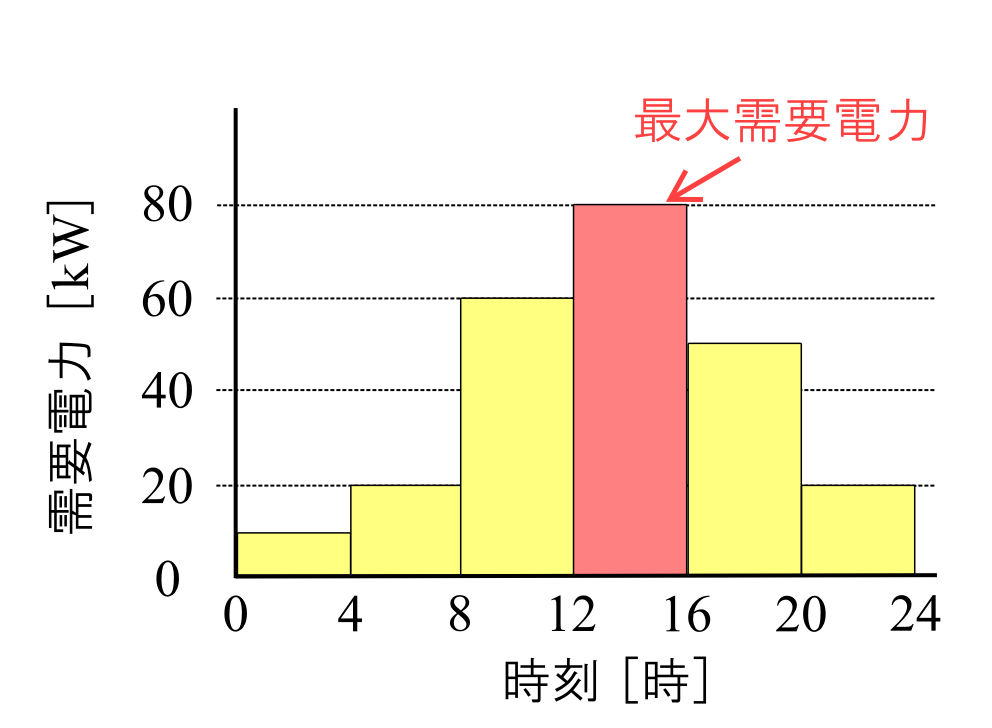
最も多く電気を使った単位時間あたりの平均電力を「最大需要電力」といいます。
ちなみに、東京電力の法人向けプランでは、30分間の平均使用電力を需要電力とし、1年で最も使用したときの需要電力の値を基準として電気料金を計算しています。
このように、最大需要電力は最大でどのくらいの電気を使用しているかの目安になります。
(2)需要率とは
ある設備で使える限界の電気の大きさを「設備容量」といいます。
この設備容量に対して、最大でどのくらい電気を使用しているのかを表すのが「需要率」です。
つまり、最大なら100%になります。それ以上だと設備がパンクします。
以下に需要率の例を記します。
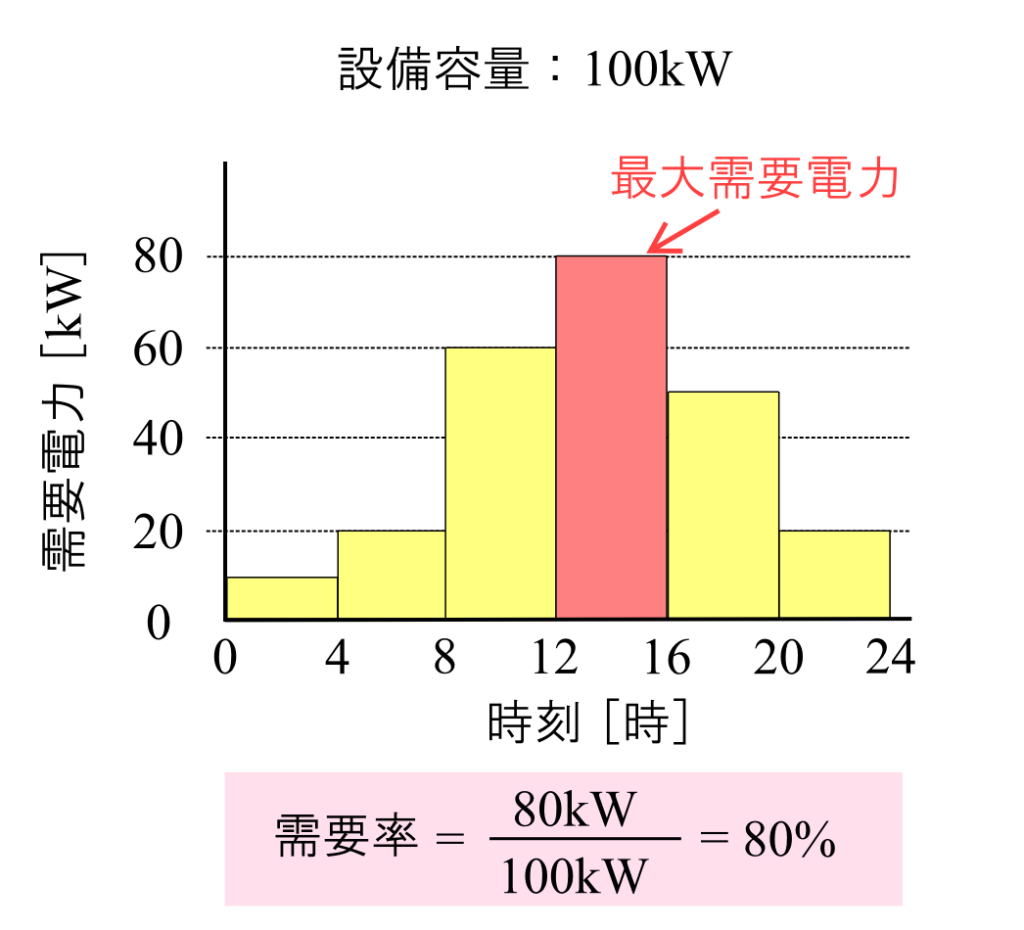
設備容量が100kWの需要家がいるとします。
24時間のうち、最も電気を使用しているのが12~16時の80kWです。
この場合の需要率は80%となります。
2.不等率
(1)合成最大需要電力
複数の需要家がいるケースを考えます。
この全需要家を1つにまとめて、そのグループとして需要電力(使用する電力)が最も多い期間を割り出します。
この期間(下記例:4時間)の電力を「合成最大需要電力」といいます。
以下に例を示します。
需要家A、Bの2つの需要家を考えます。
-1024x784.png)
-1024x784.png)
需要家Aが最も電気を使っているのは12〜16時で80kWです。
一方の需要家Bが最も電気を使っているのは16〜20時で60kWと、需要家Aと時間が異なります。
そこでそれぞれの需要電力を足し合わせます。
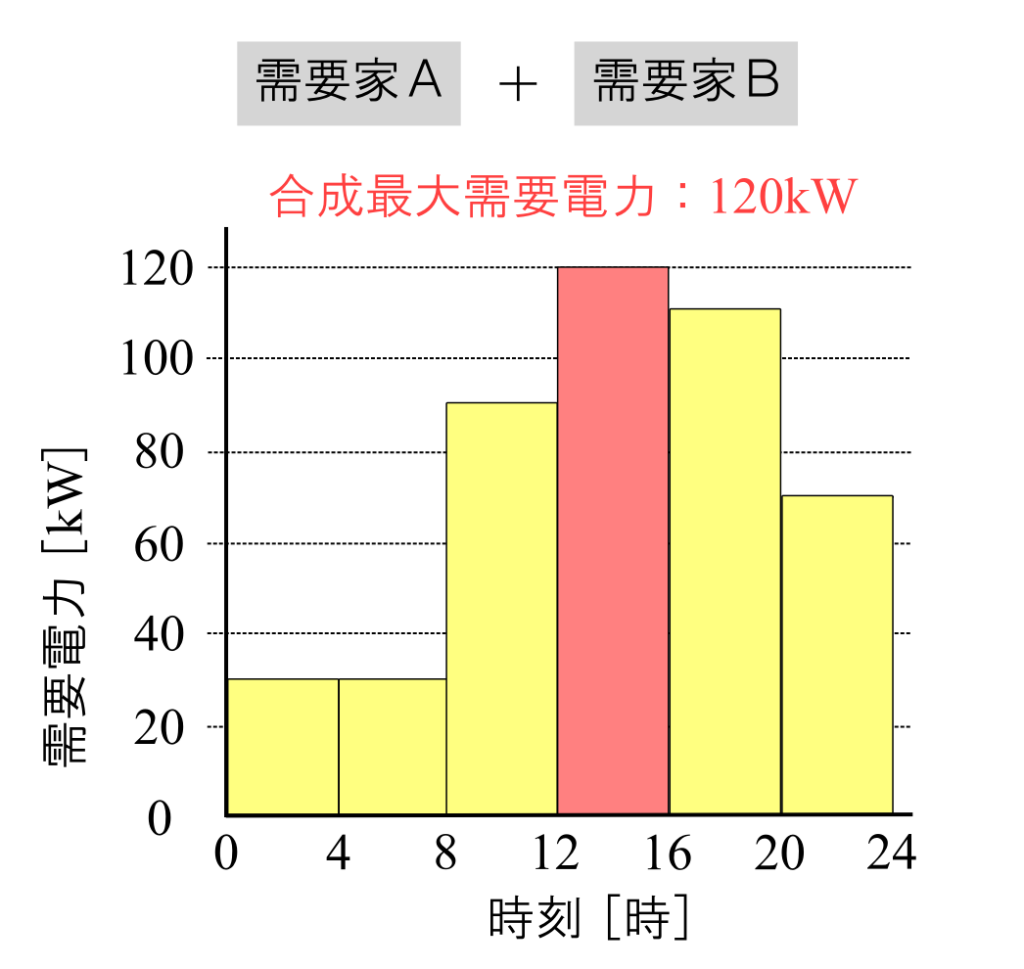
合成した需要電力を見ると、12〜16時では合わせて120kW、18〜20時では合わせて110kWです。
このことから合成最大需要電力は120kWだとわかります。
(2)不等率とは
「不等率」と言葉を聞いてもわかりにくいかもしれません。
不等率とは「複数の需要家で、合成最大需要電力に対する、それぞれの最大電力の合計の割合」になります。
複数の需要家を1つのグループとしてみなし、最も電気を使っている期間が「合成最大需要電力」でした。
しかし、それぞれの需要家では需要電力が最大になるタイミングは異なります。
(先の例では12〜16時と16〜20時)
不等率は、この最大になるタイミングが「等しくない」割合ともいえます。
先ほどの例では、合成最大需要電力が120kWですが、それぞれの最大需要電力は80kWと60kWで140kWです。
このとき、不等率は個々の需要家の最大需要電力の合計を合成最大需要電力で割って求められます。
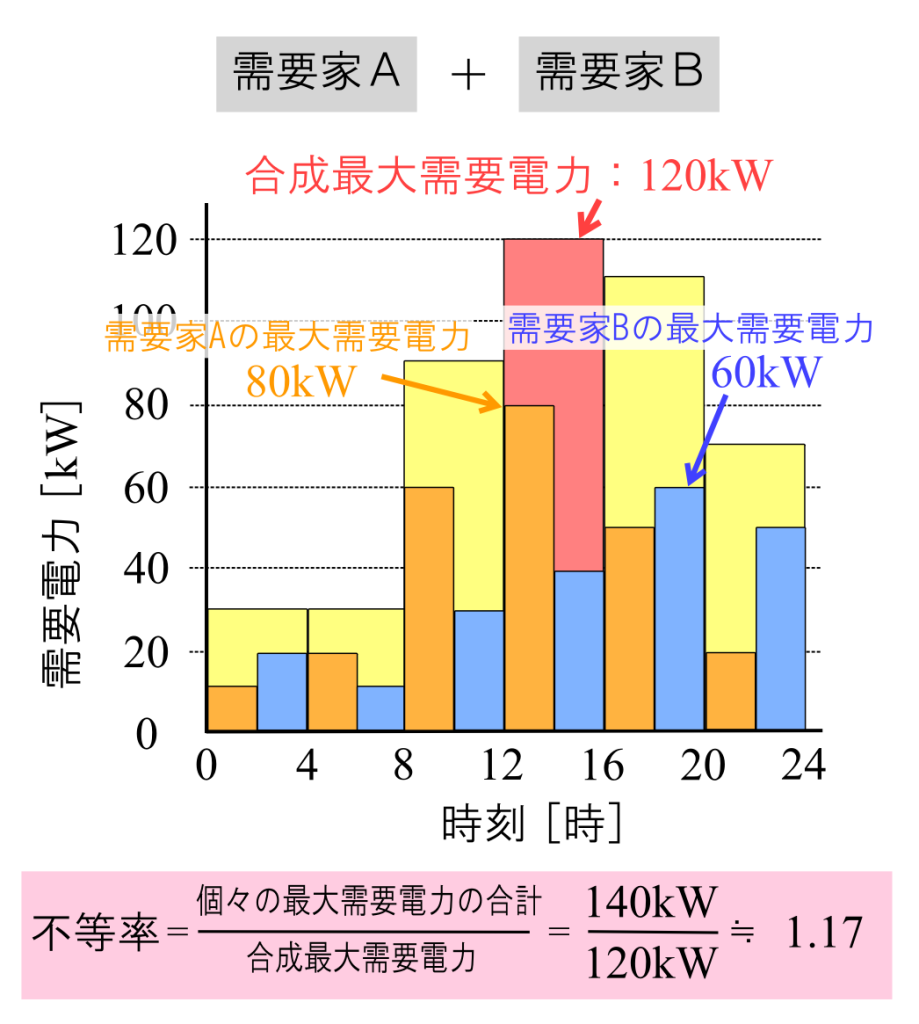
式としては、以下のようになります。
不等率は必ず1以上になります。
3.負荷率
(1)平均需要電力とは
需要電力の、ある期間における平均値を「平均需要電力」といいます。
例えば、1日において朝晩はあまり電気を使わないが、日中は多く使うという場合、24時間で割ることで1日の1時間当たり平均需要電力を求めることができます。
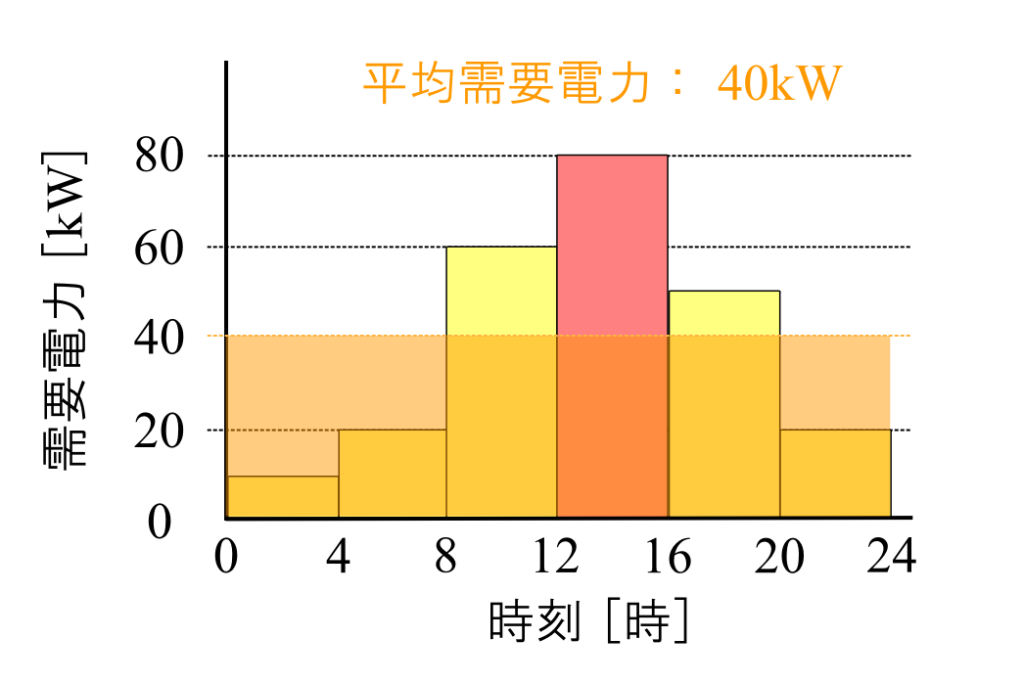
(2)負荷率とは
最大需要電力に対して平均需要電力がどのくらいかを表すのが、「負荷率」です。
時間によって使う電力の差が激しい(最大需要電力と平均需要電力の差が大きい)場合は、負荷率は小さくなります。
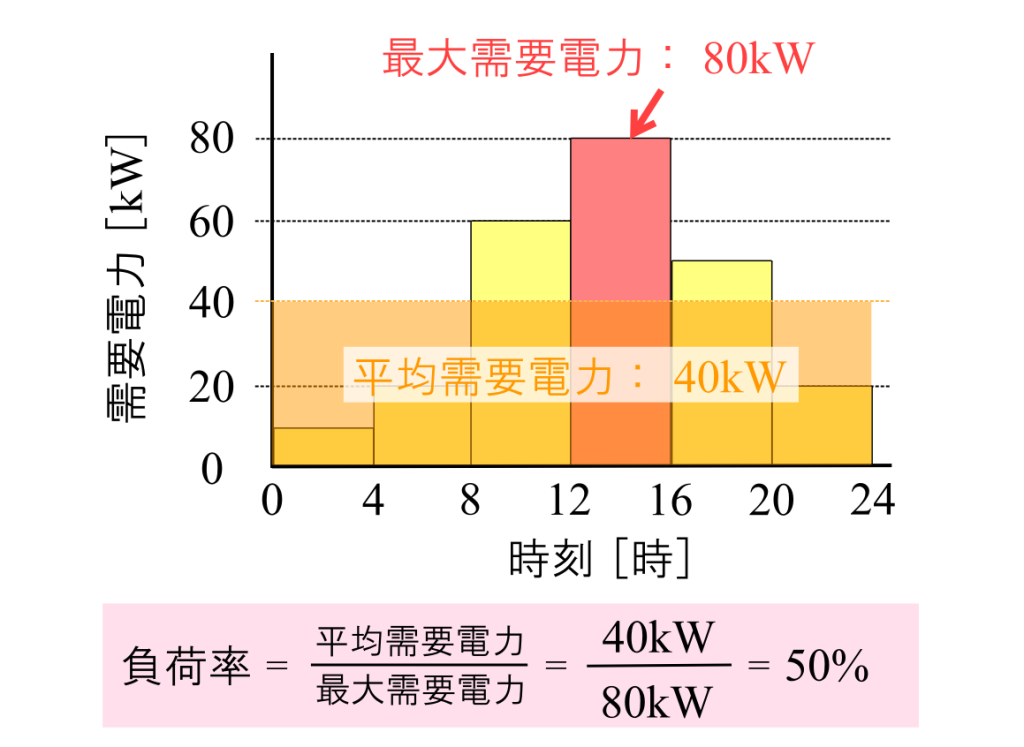
式で表すと以下の通りです。
(3)総合負荷率とは
複数の需要家がいる場合、これを1つのグループとして考え、そのグループの平均需要電力が合成最大需要電力に対してどのくらいかを表すのが、「総合負荷率」です。
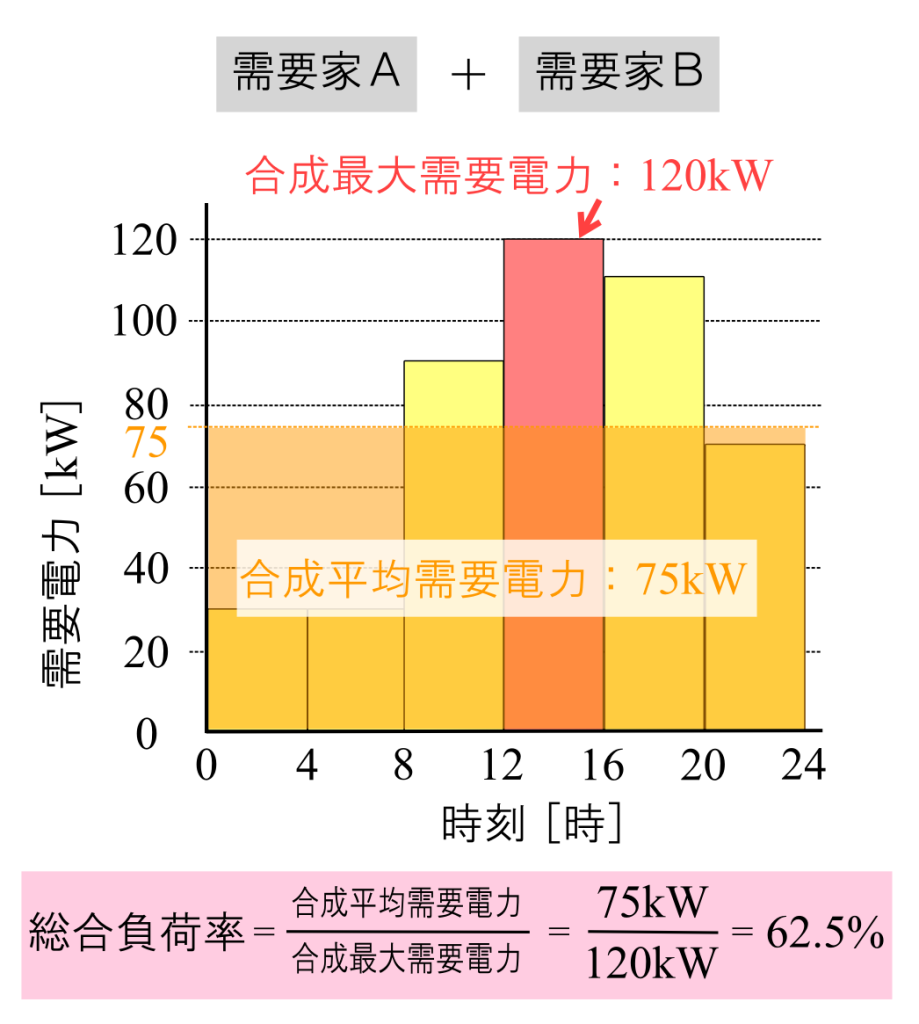
式で表すと以下の通りです。
4.例題
図のような日負荷曲線を持つA、Bの需要家がある。この系統の不等率は。
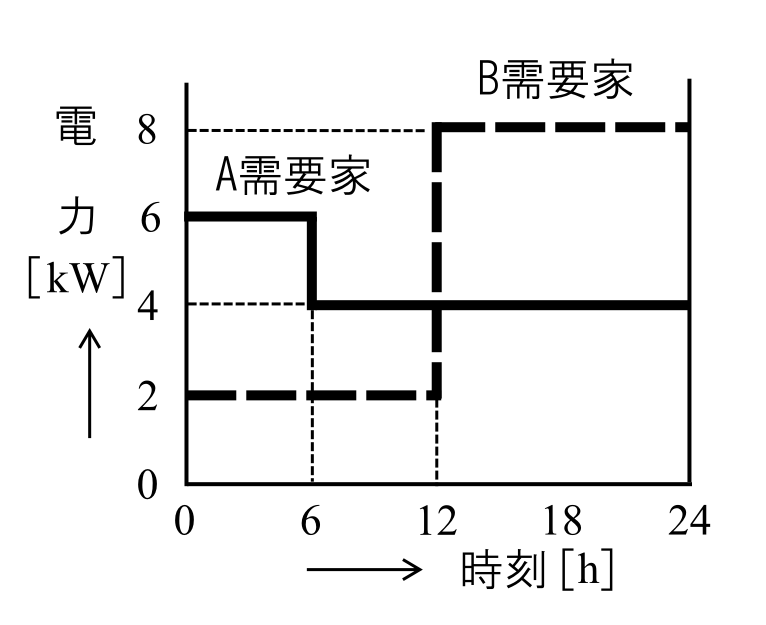
イ.1.17 ロ.1.33 ハ.1.40 ニ.2.33
答え:イ
【解説】
不等率=\(\displaystyle\frac{個々の需要家の最大需要電力の合計}{合成最大需要電力}\)
のため、A、Bそれぞれの最大需要電力と合成最大需要電力を求めます。
最大需要電力はA需要家が\(6\)[kW]、B需要家が\(8\)[kW]です。
合成最大需要電力は、B需要家が\(8\)[kW]、A需要家が\(4\)[kW]使用している12~24時の12時間です。
そのため、合成最大需要電力は\(8+4=12\)[kW]となります。
よって不等率は
\(\displaystyle\frac{(6+8)}{12}≒1.17\)となります。
設備容量が400kWの需要家において、ある1日(0~24時)の需要率が60%で、負荷率が50%であった。
この需要家のこの日の最大需要電力\(P_M\)[kW]の値と、この日1日の需要電力量\(W\)[kW・h]の値の組み合わせとして、正しいものは。
イ.\(P_M=120\) \(W=5760\) ロ.\(P_M=200\) \(W=5760\)
ハ.\(P_M=240\) \(W=4800\) ニ.\(P_M=240\) \(W=2880\)
答え:ニ
【解説】
需要率[%]=\(\displaystyle\frac{最大需要電力}{全設備容量}×100\)
より、最大需要電力が求められます。
わかっている値を代入して計算すると
\(60=\displaystyle\frac{最大需要電力}{400}×100\)
\(最大需要電力=\displaystyle\frac{60×400}{100}=240\)[kW]
負荷率[%]=\(\displaystyle\frac{平均需要電力}{最大需要電力}×100\)
より、平均需要電力が求められます。
わかっている値を代入して計算します。
\(50=\displaystyle\frac{平均需要電力}{240}×100\)
\(平均需要電力=\displaystyle\frac{50×240}{100}=120\)[kW]
ここでの平均需要電力は1時間あたりの平均電力なので、時間をかけることでその期間の電力量が求められます。
1日は24時間なので、
\(120×24=2880\)[kW・h]となります。
5.まとめ
以下に公式をまとめます。
これらの式を変形して色々求められるようになることがポイントです。
需要率[%]=\(\displaystyle\frac{最大需要電力}{全設備容量}×100\)
不等率=\(\displaystyle\frac{個々の需要家の最大需要電力の合計}{合成最大需要電力}\)
負荷率[%]=\(\displaystyle\frac{平均需要電力}{最大需要電力}×100\)
総合負荷率[%]=\(\displaystyle\frac{合成平均需要電力}{合成最大需要電力}×100\)
<<その他の電気理論などはこちらのページをご確認ください。>>