【電気を学ぶ】電磁気学④　電磁誘導（自己誘導とコイルのエネルギー）

１．自己誘導

（１）自己誘導と自己インダクタンス

コイルには磁束の変化を妨げる方向に電流を流す性質があることを学びました。

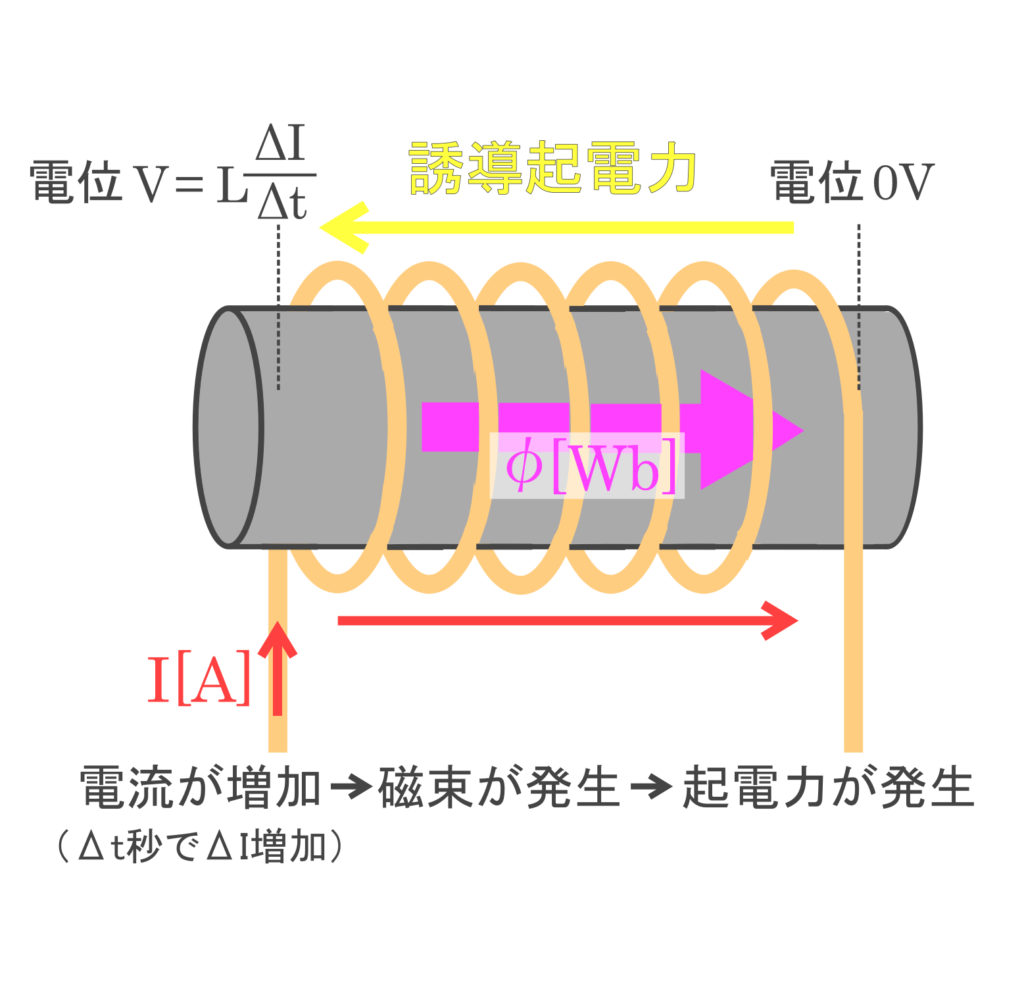
そこで、今回は図のようなソレノイドコイル（円筒型のコイル）に電池がつながっている状況を考えます。

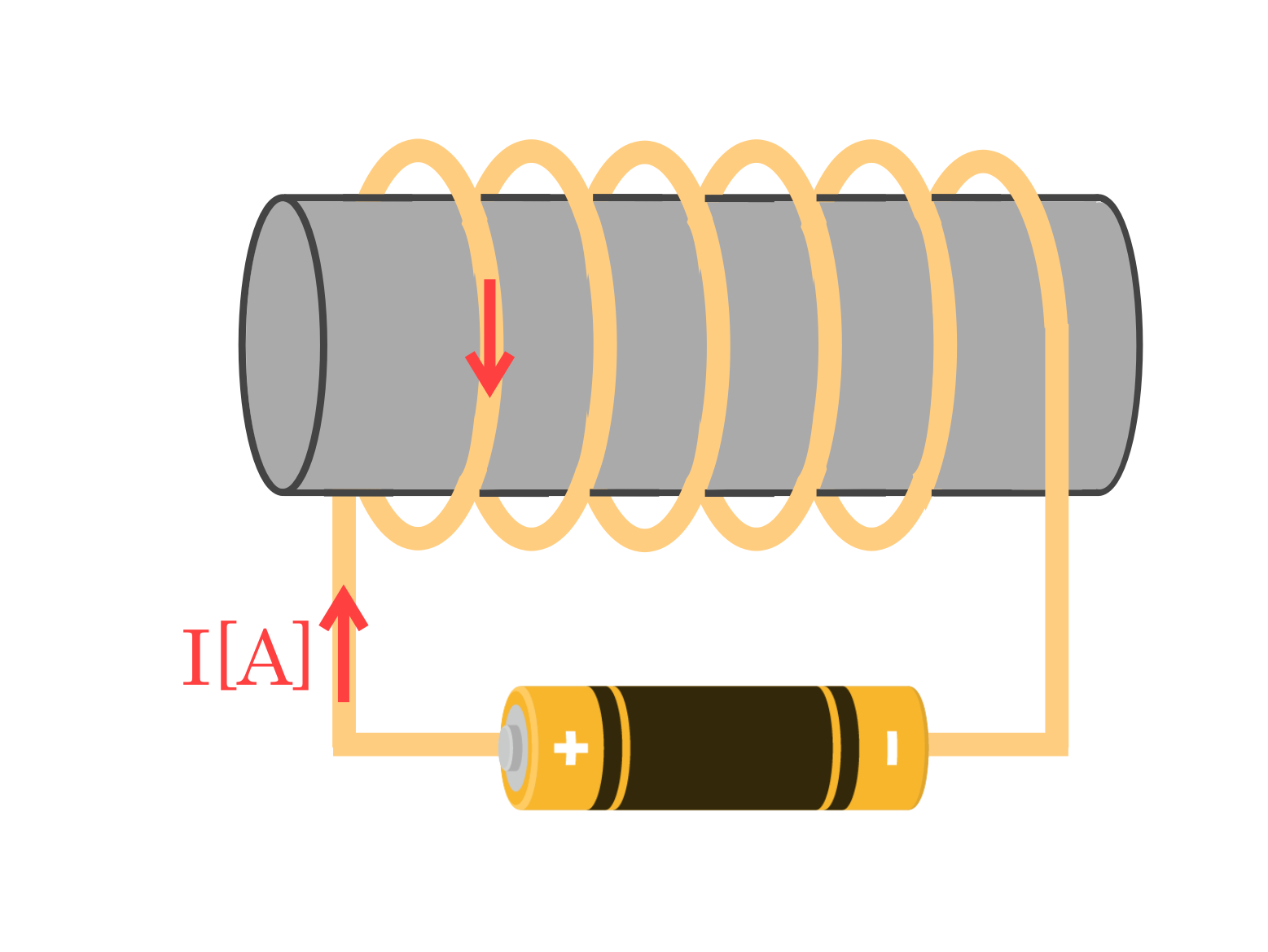
ここで、矢印の方向に電流 \(I\) \([A]\) を流します。

導体に電流が流れたことにより、ソレノイドコイルを貫く磁束 \(φ\) \([Wb]\) が発生します。

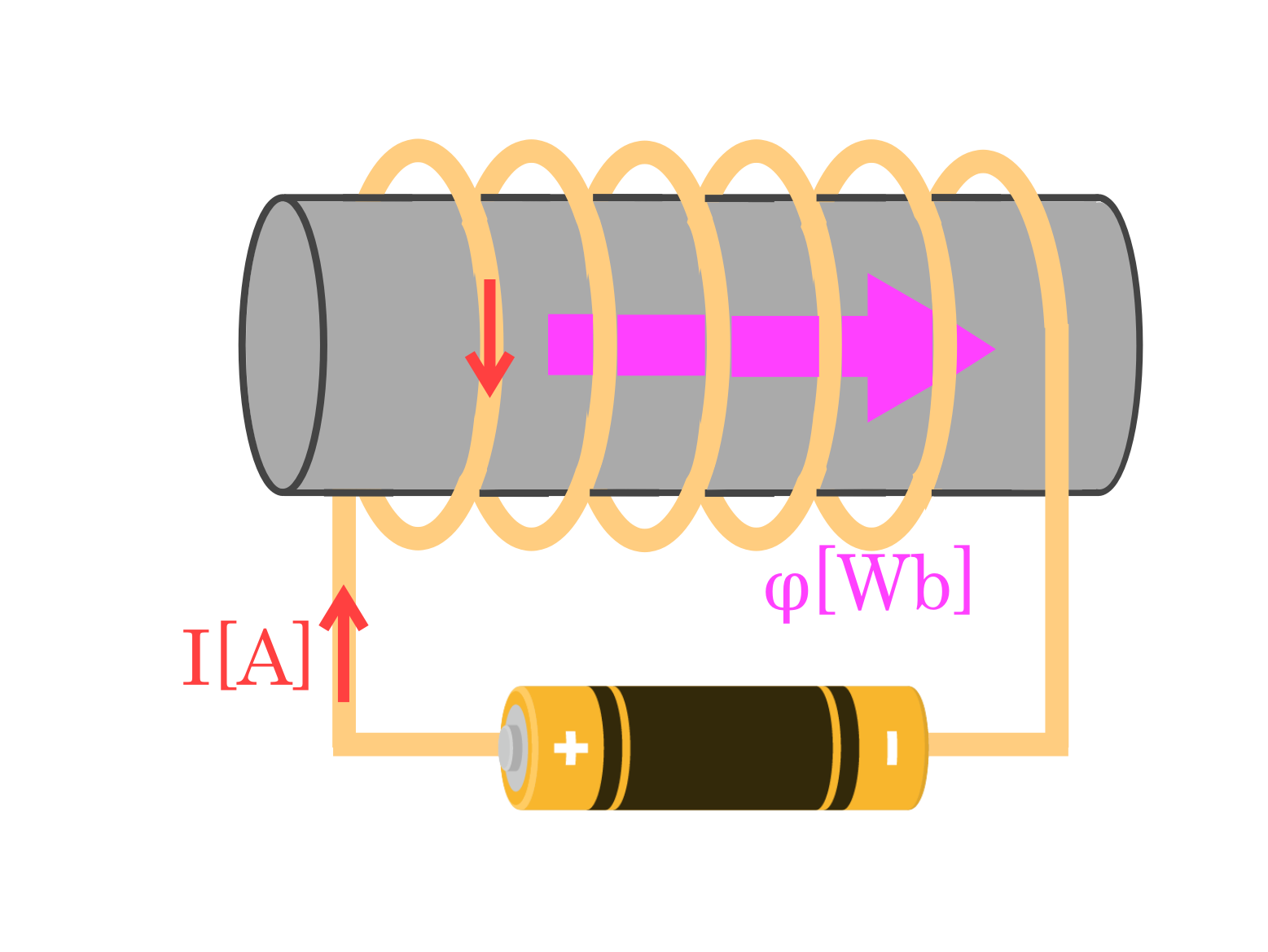
コイルを貫く磁束が変化したことで、ソレノイドコイルには磁束の変化を妨げる方向に誘導起電力が発生します。

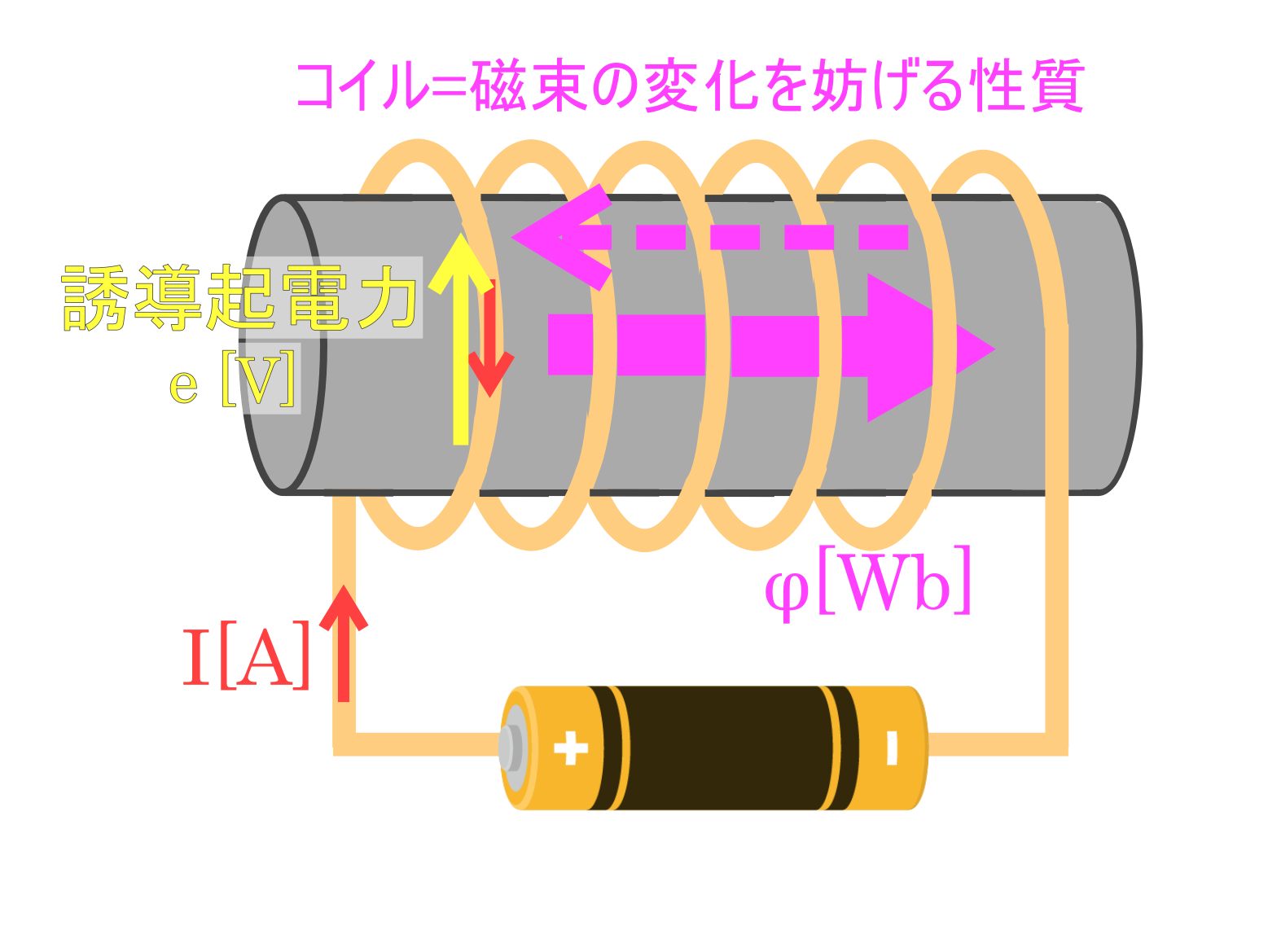
この誘導起電力の向きは、流した電流の向きとは逆向きになります。

このような、コイルに電流が流れるとき、その流れと反対の向きに起電力が発生することを自己誘導といいます。

コイル自身がきっかけで起電力が発生するため、「自己」誘導といいます。

微小な時間に微小な電流が流れることで発生する起電力のため、この起電力は比例定数 \(L\) をかけて以下のように表します。

比例定数 \(L\) は 自己インダクタンス といい、単位 \(H\)（ヘンリー）で表します。

式にマイナスがつくのは、ファラデーの法則と同じく、磁束変化を「妨げる向き」という意味です。

また、誘導起電力 \(e\) は磁束 \(φ\) で表すと、\(\displaystyle{e=-N×\frac{Δφ}{Δt}}\)となります。

そのため、自己インダクタンス\(L\)は以下のように表すことができます。

\(\displaystyle{-L×\frac{ΔI}{Δt}=-N×\frac{Δφ}{Δt}}\)

\(\displaystyle{L=N×\frac{Δφ}{Δt}×\frac{Δt}{ΔI}}\)

\(\displaystyle{L=N\frac{φ}{I}}\)

（２）環状コイルの自己インダクタンス

図のような円環状の鉄心に巻いたコイル（環状コイル）の自己インダクタンスについて考えます。

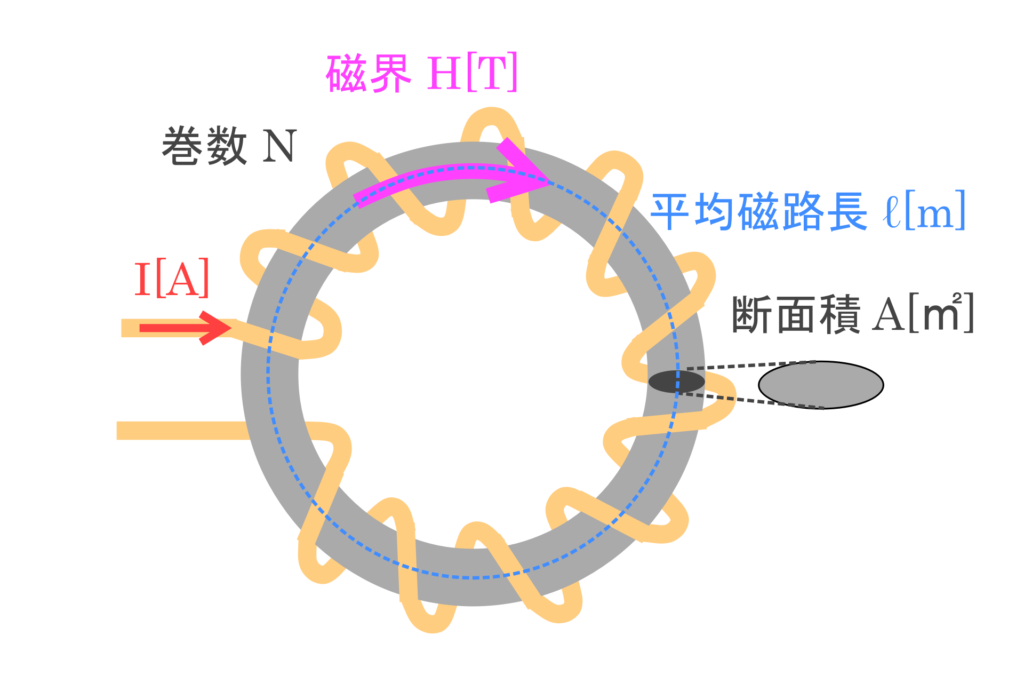
まず、自己インダクタンスを表す式　\(\displaystyle{L=\frac{Nφ}{I}}\)について

この式の中の磁束 \(φ\) を磁界の強さ \(H\) を使って表すことを考えます。

磁束 \(φ\) は磁束密度 \(B\) と、通過する面積 \(A\) の積として表せます。

\(φ=BA\)

磁束密度 \(B\) は磁界の強さ \(H\) と透磁率 \(μ\) の積なので、以下の式が成り立ちます。

\(φ=BA=μHA\)　・・・①

そして、巻数が \(N\) 回、導体の長さ \(ℓ\ [m]\) のソレノイドコイルに、電流 \(I\ [A]\) を流した時の単位長さあたりの磁界の強さ \(H\ [T]\) は、以下の式で表します。

\(\displaystyle{H=\frac{NI}{ℓ}}\)　・・・②

式①、②を自己インダクタンス \(L\) の公式\(\displaystyle{L=\frac{Nφ}{I}}\)に代入します。

\(\displaystyle{L=N\frac{φ}{I}}\)

　\(\displaystyle{=N\frac{μHA}{I}}\)

　\(\displaystyle{=N\frac{μNIA}{Iℓ}}\)

　\(\displaystyle{=\frac{μAN^2}{ℓ}}\)

透磁率 \(μ\)を、真空の透磁率 \(μ_0\)、比透磁率 \(μ_r\)と分けることで以下のようにも表せます。

\(\displaystyle{L=\frac{μ_0μ_rAN^2}{ℓ}}\)

２．相互誘導

コイルが２つの場合、相互誘導という現象が起きます。

図のように、1次コイルに電流を流すと、1次コイルには右ねじの法則の向きに磁束が発生します。

このとき、2次コイルでも同様に磁束が増加します。

そして2次コイルでは、この磁束の増加を妨げる方向に起電力が発生することになります。

2次コイルは1次コイルの変化のせいで起電力を発生させるので、このような現象を「相互」誘導といいます。

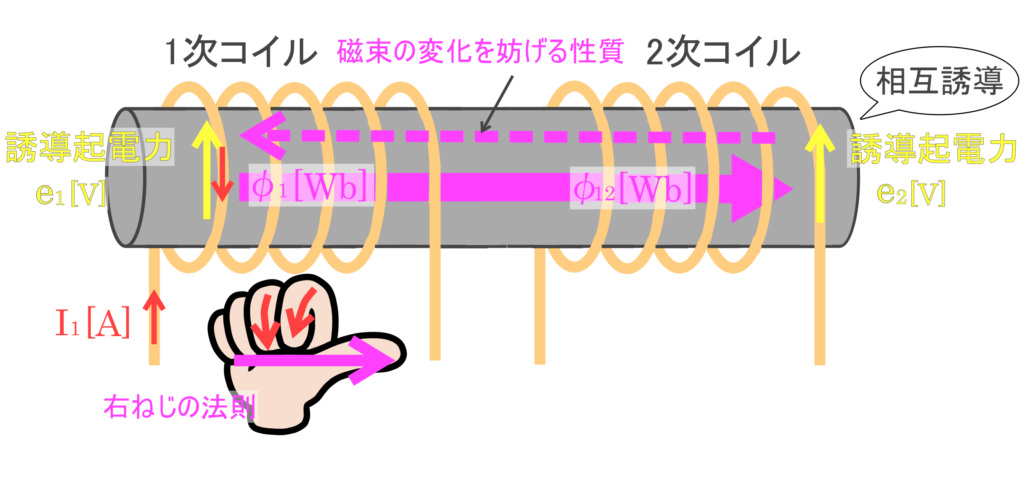
これは変圧器の原理にもなっています。

一次コイルを通る磁束は、全て2次コイルを通るわけではありません。

1次コイルのみ通過する磁束は漏れ磁束といいます。

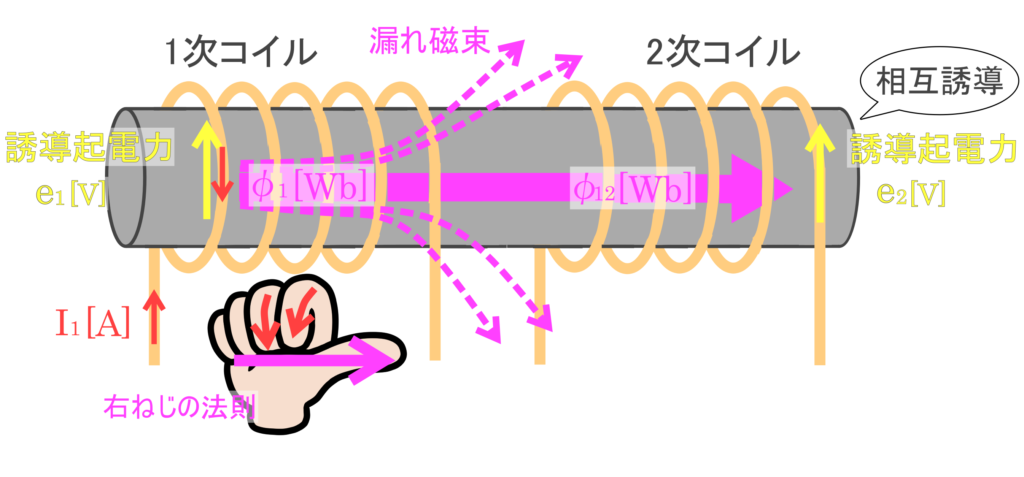
2次コイルに発生する起電力は1次コイルの電流\(I_1\)と、比例定数\(M\)を使って以下のように表します。

\(\displaystyle{e_2=-M×\frac{ΔI_1}{Δt}}\)

比例定数\(M\)は相互インダクタンスといい、単位は\(H\)（ヘンリー）を使います。

また、相互インダクタンス\(M\)は1次コイル、2次コイルそれぞれの自己インダクタンスを使っても表すことができます。

自己インダクタンス\(L_1\)と\(L_2\)のコイルを接続したとき、２つのインダクタンスを合わせたインダクタンスを合成インダクタンスといいます。

合成インダクタンスは自己インダクタンス\(L_1\)、\(L_2\)と、相互インダクタンス\(M\)を使って表すことができます。

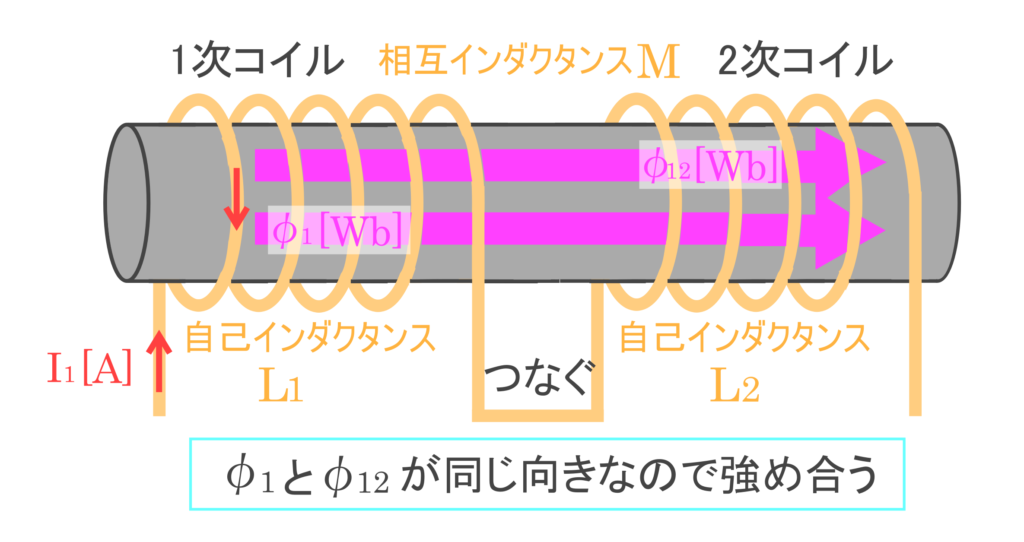
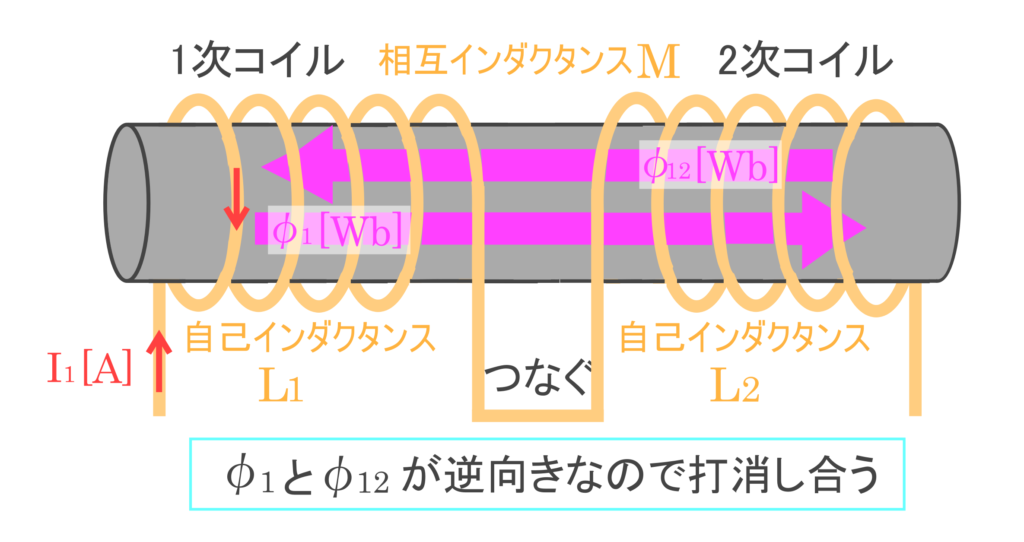
合成インダクタンスは接続の仕方で、和動接続と差動接続に分けられます。

３．コイルに蓄えられる電磁エネルギー

ソレノイドコイルに電流を流すと逆起電力が発生します。

このとき、図のようなコイルの右側を\(0V\)とすると、左側は\(\displaystyle{e=L×\frac{ΔI}{Δt}\ [V]}\)となります。

「電位」は\(+1[C]\)の電荷が持つ位置エネルギーとみなせます。

コイルの左側で位置エネルギー \(U_r\) は \(Ur=QV\ [J]\) でしたが

右側の位置エネルギー \(U_l\) は \(U_l=Q×0\ [J]\) へと減少しています。

電流が流れると磁界が発生することから、

この失われたエネルギーは電磁エネルギーと考えることができます。

下のグラフは時間 \(t[s]\) と電流 \(I[A]\) の変化を表しています。

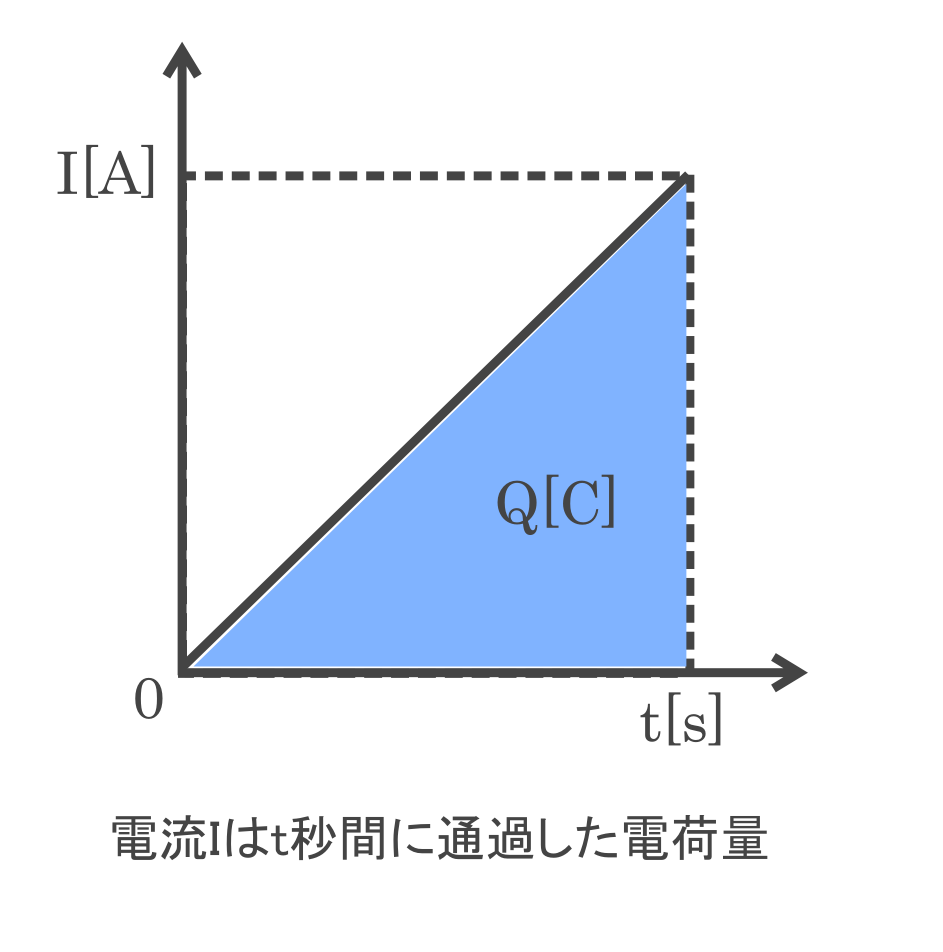
グラフのように時間 \(t(s)\) が経過するにつれて電流 \(I[A]\) が増える場合、

青く塗りつぶした面積が、コイルを通過した電荷量 \(Q[C]\)（時間当たりの電荷量）になります。

式にすると以下のようになります。

\(Q=\displaystyle{\frac{1}{2}×It}\)

起電力は\(e=\displaystyle{L×\frac{I}{t}}\) なので

失われた位置エネルギー \(QV\) は、コイルに蓄えられていた電磁エネルギーとみなせるので、以下のようになります。

\(\displaystyle{QV=W=\frac{1}{2}×It×L×\frac{I}{t}= \frac{1}{2}×LI^2\ [J]}\)

４．まとめ

今回は、自己誘導とコイルのエネルギーについて解説しました。

以下に、記事で紹介した公式をまとめておきます。