

複雑な回路の計算で欠かせない、キルヒホッフの法則。
例題も含めて解説していきます。
そのほかの電気理論の解説については、こちらのカテゴリーで公開しております。
1.キルヒホッフの法則とは?
キルヒホッフの法則は、回路計算をする上で欠かせない重要な法則です。
第一法則と第二法則があり、それぞれ電流則、電圧則とも呼ばれるように、電流と電圧に関する法則です。
(1)キルヒホッフの法則(第一法則)
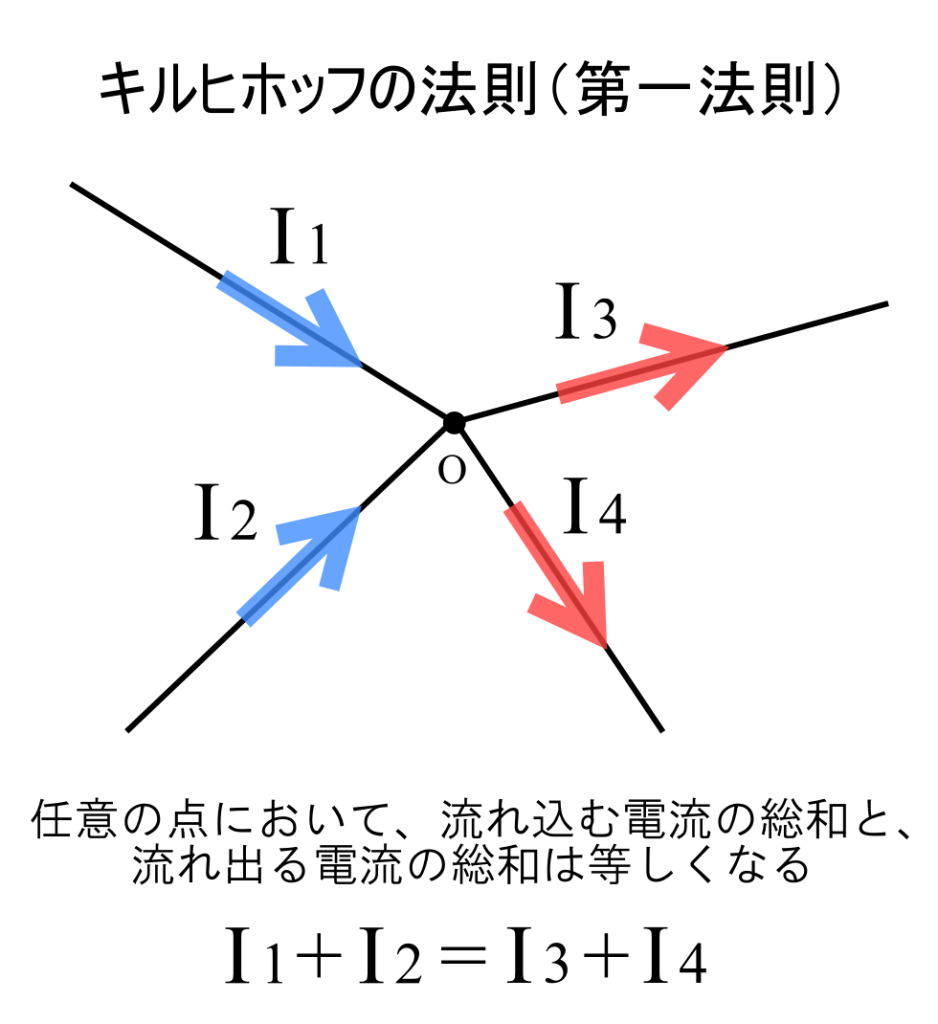
上の図では、\(I_1\)と\(I_2\)は点Oに流れ込んでいて、\(I_3\)と \(I_4\)は流れ出ています。
このとき、以下の式が成り立ちます。
\(I_1+ I_2= I_3+ I_4\)
流れ込む電流の総和と流れ出る電流の総和は等しくなります。
この式を変形すると以下の式も成り立ちます。
\(I_1+ I_2-I_3-I_4=0\) (総和はゼロ)
つまり、向きを考慮すると点Oに流れ込んだり、流れ出ている電流はすべて足すとゼロになります。
電流は水の流れに例えられることが多いですが、流れ込む水と流れ出る水の水量が同じと考えればイメージしやすいかと思います。

(2)キルヒホッフの法則(第二法則)
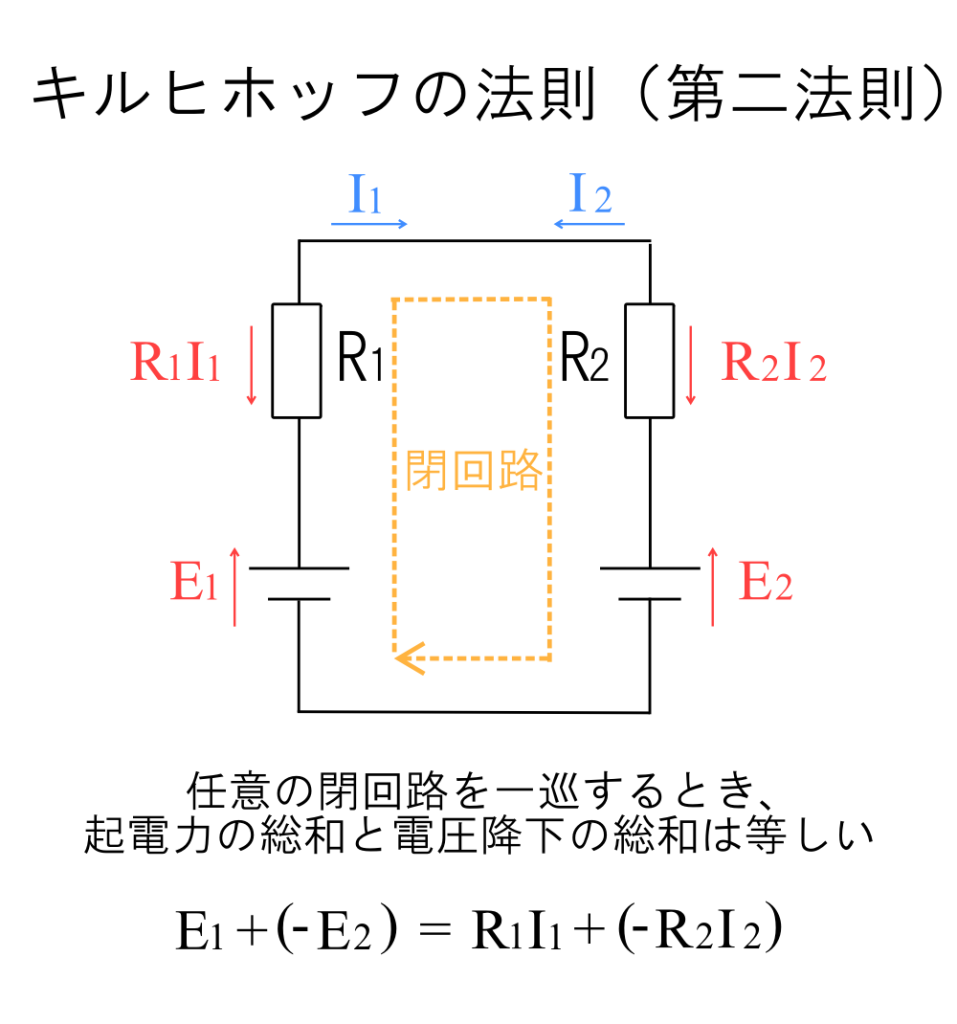
このような閉回路において、起電力\(E_1\)と\(E_2\)の合計と、電圧降下\(R_1I_1\)と\(R_2I_2\)の合計は等しくなります。
閉回路の方向に注目すると、二つの起電力の向きは逆です。そのため、\(E_2\)の符号はマイナスになります。
同様に、電圧降下の向きも逆なので\(R_2I_2\)の符号はマイナスとして計算します。
この式を変形すると以下の式も成り立ちます。
\(E_1-E_2-R_1I_1+R_2I_2=0\)(総和はゼロ)
向きを考慮すると閉回路中の起電力と電圧降下のすべてを足すとゼロになります。
電圧降下は電圧が下がることなので、電圧を生み出す起電力とは符号が反対になります。
電圧の法則も水の流れに例えるとイメージしやすいです。
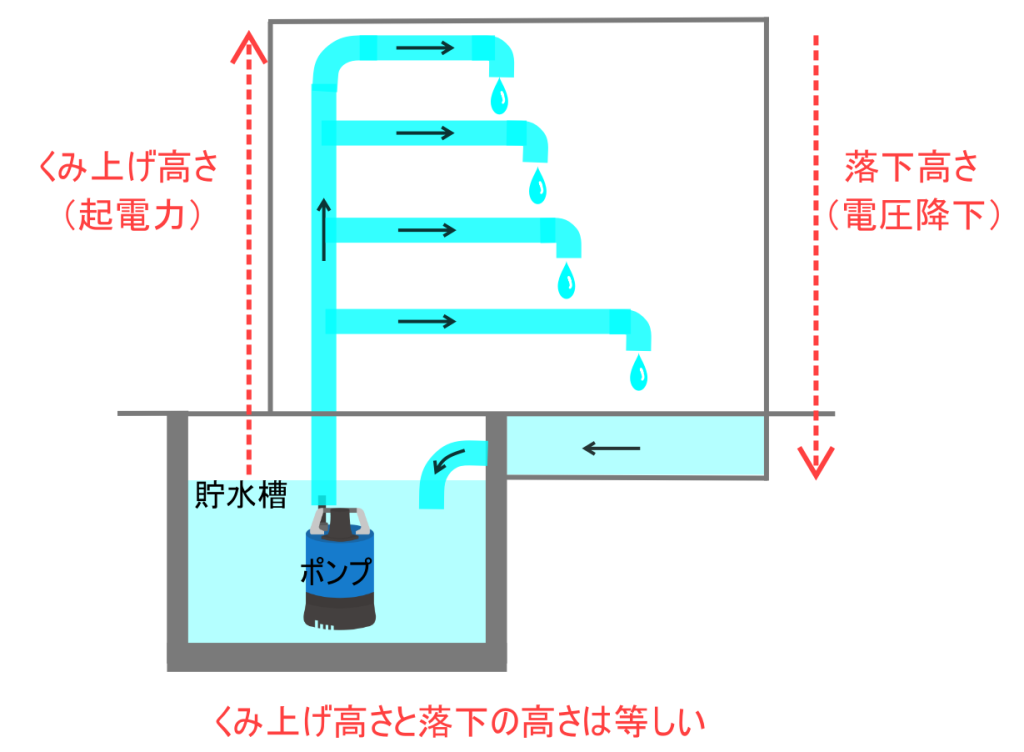
貯水槽から水をくみ上げ、最終的に水が貯水槽に戻る状況を考えます。(噴水やプールなど)
くみ上げる高さを起電力、落下する高さを電圧降下と考えると、これらが等しくなることがイメージできると思います。
2.例題(第一種電気工事士試験より)
キルヒホッフの法則を使う問題が過去に出題されています。
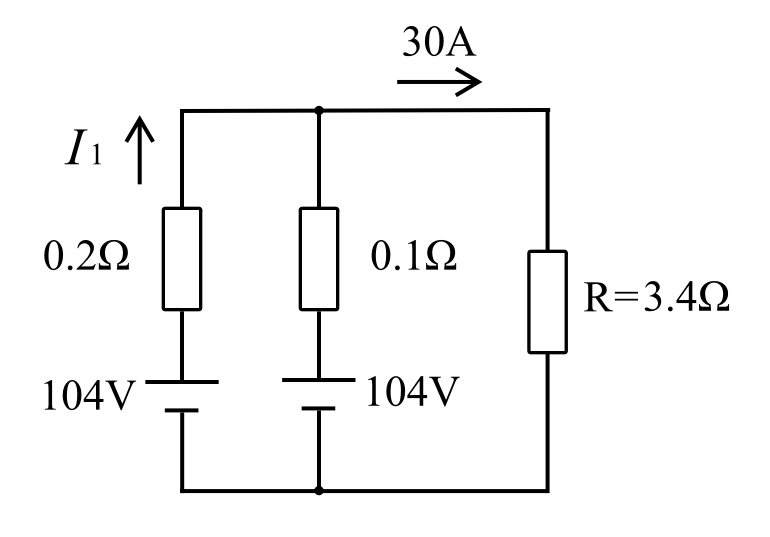
図のような直流回路に置いて、抵抗\(R=3.4Ω\)に流れる電流が\(30A\)であるとき、図中の電流\(I_1\)[A]は。
イ.5 ロ.10 ハ.20 ニ.30
答え:ロ
【解説】
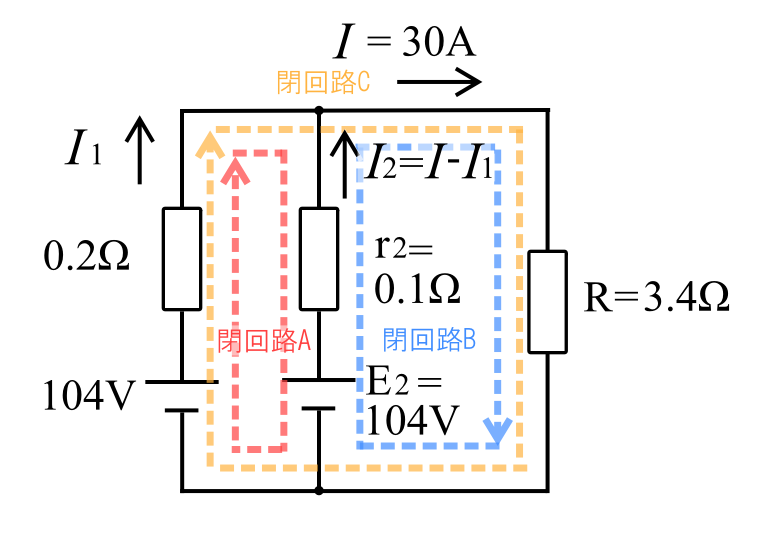
複雑に見える回路ですが、図のように回路を閉回路A、B、Cと分けて考えます。
抵抗\(r_2\)を流れる電流は第一法則から、\(I_2=I-I_1\)と表すことができます。
閉回路Bにおいてキルヒホッフの法則の第二法則を使うと
\(E_2=r_2×(I-I_1)+RI\)
となります。
わかっている数値を代入すると
\(104=0.1×(30-I_1)+3.4×30\)
\(-0.1I_1=104-3-102\)
\(I_1=10\)
よって答えは10[A]となります。


