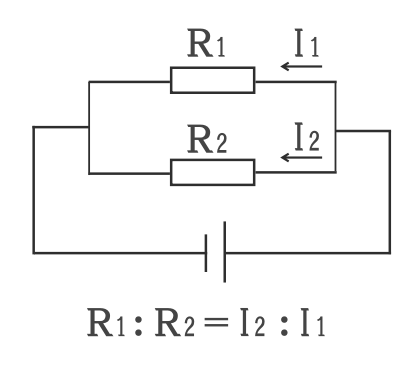
１．分流の法則（抵抗が２つ）
（１）抵抗２つに分流する比率は抵抗の逆比になる
並列回路において、複数に分岐して流れる電流はその抵抗値の逆比になります。
抵抗の比が \(R_1\)：\(R_2\) の場合、 電流の比は \(I_2\)：\(I_1\) となる
\(R_1\)：分岐回路1の抵抗値 \(R_2\)：分岐回路2の抵抗値 \(I_1\)：分岐回路1の電流値 \(I_2\)：分岐回路2の電流値
（２）なぜ逆比になるのか？
ここで例題を解いてみます。
以下のような直流並列回路を考えます。
以下の回路において、抵抗\(3\)Ωと抵抗\(6\)Ωのそれぞれに流れる電流\(I_1\)、\(I_2\)の値は？
解答：\(I_1=4\)[Ａ]、\(I_2=2\)[Ａ]
【解説】
回路の合成抵抗は和分の積より
\(R\) [Ω]\(=(3×6)÷(3+6)\)
\(=18÷9\)
\(=2\) [Ω]
となり、合成抵抗は\(2\)[Ω]と求められます。
回路全体に流れる電流\(I\)[Ａ]はオームの法則より
\(I\)[Ａ]＝\(12\)[Ｖ]÷\(2\)[Ω]＝\(6\)[Ａ]
となり\(6\)[Ａ]となります。
ここで、電流\(I\)は抵抗\(3\)Ωがある回路と抵抗\(6\)Ωのある回路へと２通りに分かれます。
並列にかかる電圧は等しいため、抵抗それぞれに流れる電流はオームの法則より、
\(I_1＝12\)[Ｖ]÷\(3\)[Ω]＝\(4\)[Ａ]
\(I_2\)＝\(12\)[Ｖ]÷\(6\)[Ω]＝\(2\)[Ａ]
となります。
解答：\(I_1=4\)[Ａ]、\(I_2=2\)[Ａ]
ここで求めた電流値を抵抗値と比較すると
\(I_1\)：\(I_2\)は\(4：2=2：1\)となっています
\(R_1\)：\(R_2\)は\(3：6=1：2\)なので、逆比になっています。
このように分岐した回路に流れる電流はその回路の抵抗値の逆比になることがわかります。
２．分流の法則（抵抗が３つ以上）
抵抗が２つの場合は、逆比を求めればいいのですが、３つ以上ある場合はどうなるか見ていきます。
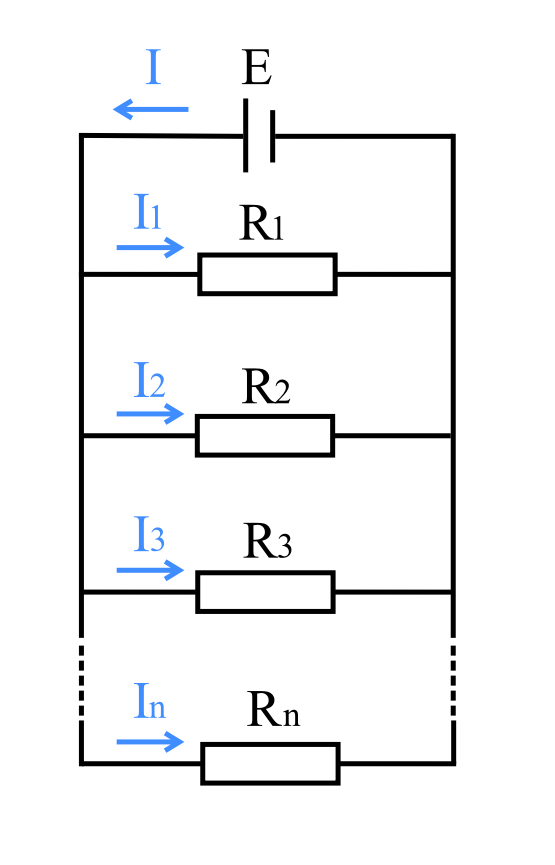
並列接続なので電圧はすべて\(E\)です。
\(R_1\)に流れる電流は、\(I_1=\displaystyle\frac{E}{R_1}\)
回路の合成抵抗を\(R_0\)とすると、\(E=I×R_0\)なのでこれを代入すると、
\(I_1=\displaystyle\frac{R_0}{R_1}×I\)となります。
\(R_2\)以下も同様です。
よって、n個の抵抗に分流する電流の大きさを求める式は以下の通りです。
\(I_1=\displaystyle\frac{R_0}{R_1}×I\)
\(I_2=\displaystyle\frac{R_0}{R_2}×I\)
\(I_3=\displaystyle\frac{R_0}{R_3}×I\)
：
\(I_n=\displaystyle\frac{R_0}{R_n}×I\)
３．例題
図のような回路で、電流計(A)の値が\(1\)Aを示した。このときの電圧計(V)の指示値[V]は。
イ．16 ロ．32 ハ．40 ニ．48
答え：イ
【解説】
\(8\)[Ω]に流れる電流を\(I_2=1\)[A]とすると、
\(4+4=8\)[Ω]に流れる電流\(I_1\)も同じく\(1\)[A]、
そして大きさが半分の\(4\)[Ω]に流れる電流\(I_3\)は\(8\)[Ω]に流れる電流の2倍大きな電流が流れるので\(2\)[A]、と計算しなくてもわかります。
そしてこれらを足し合わせた電流\(I=4\)[A]が\(4\)[Ω]の抵抗に流れます。
この電圧降下が電圧計に示されます。
よって、電圧計の指示値はオームの法則より
\(V=4×4=16\)[V]と求められます。
この分流の法則は電気工事士試験はもちろん、電験３種でも使うような重要な知識となります。
受験を検討している方は覚えておきましょう。
その他、電気を学ぶ記事はこちらから。
